Директен и обратна пропорционалност 1

В предишните уроци сме научили частично пропорция. В този урок ще се въведат нови понятия като пряка пропорционалност и обратна пропорционалност.

пряко пропорционално

Да разгледаме следния пример. Човек изяжда по една минута два орех:

1 минути - 2 орех

2 минути и същи човек яде два пъти по-ядки, т.е. 4 орех.

2 минути - 4 орехови

Лесно е да се види, че увеличаването на времето на двукратния размер яде ядки, също се е удвоил.

Сега се намали времето от две минути до една минута. След това се оказва, че една минути, което човек яде гайка 2.

1 мин - 2 орех

Лесно е да се види, че с намаляване на времето два пъти сумата, яде ядки също наполовина.

Директен пропорционалност се крие във факта, че увеличението на магнитуд няколко пъти, другите се увеличава със същия коефициент. И обратното. Когато намаляване магнитуд няколко пъти, другите намалява със същия коефициент.

В първия случай, ние увеличихме времето от една минута, за да две минути. В резултат на това количеството изяден гайките се е увеличил в пряка зависимост от това е двойна.

Във втория случай, напротив, ние намалихме времето от две минути до една минута. В резултат на това количеството изяден ядки намаляват правопропорционално на която е двойна.

Примерите, които са разгледани по-горе, а именно:

са пропорции. Ако премахнете думи минута и ядки. очевидно е, че това равенство на две отношения, в които работата на членовете на крайност е продукт на средния представител.

Всеки съставен дял трябва да бъде проверен от дясно или не. Ако продуктът на екстремните членовете на част е продукт на средния представител, като част е вярна.

Нека да покажат на пропорциите, които направихме в изследването на пряка пропорционалност:

Ярък пример е директно пропорционална разстояние. Например, ако човек се движи със скорост от 2 километра в час (км / ч), а след това за един час, той заема два километра:

S = о х т = 2 km / h х 1 час = 2 км

Но, ако се увеличи скоростта на, например два пъти - за да стане равна на 4 километра в час, същите един часа хората ще вземат два пъти разстоянието:

S = о х т = 4km / h х 1 час = 4 км

Тя може да се види, че с увеличаване на скоростта на два пъти разстоянието се удвоява.

обратен

Да разгледаме следния пример. В колоездач от дома си към спортната площадка при скорост от 20 km / h пристига в 6-та минута

20 km / h - 6-та

Ако скоростта на движение да се удвои, т.е. за да стане равна на 40 km / h, а след това по същия път колоездач ще похарчи половината от времето, т.е. 3 минути:

40 km / ч = 3 минути

Лесно е да се забележи, че скоростта се увеличава два пъти, времето движение намаляват със същия коефициент, който е два пъти:

Сега намали скоростта от 40 km / h до 20 km / h. Speed ​​наполовина. В резултат на това, времето за движение увеличава със същия коефициент:

20 km / h - 6-та

Лесно е да се види, че когато скоростта се намалява наполовина, а трафикът се е увеличил със същия коефициент, който е два пъти:

Обратен пропорционалност се крие във факта, че увеличението на магнитуд няколко пъти, другите намалява със същия коефициент. И обратно - намаление с една стойност в рамките на няколко пъти, а другите се увеличава със същия коефициент.

Фразата "обратно пропорционална" говори за себе си. Фактът, че увеличението на стойността на един, другите намалява, т.е. Той действа обратно на тази стойност. При скорост от 20 km / h колоездач пристига в продължение на 6 минути, докато увеличаване на скоростта на 40 km / h пристига в продължение на 3 минути. Това означава, че стойността на скоростта и времето са обратно пропорционални. С увеличение от един - на останалите намалява. И обратното. С намаляване на едно - останалите се увеличава.

И ако стойностите са обратнопропорционални, стойностите отношението магнитуд равни на обратното съотношение на съответните стойности от различен мащаб. Какво означава това?

Фактът, че примерите, които сме считани за по-горе, а именно:

в действителност, пропорциите не са. Тъй като продуктът на екстремните членове не е равна на произведението на средния представител.

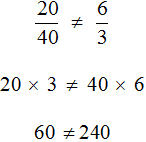
Нашите ценности са обратнопропорционални и в двата аспекта. се казва в обратен имот, който, ако стойностите са обратнопропорционални, стойностите отношението магнитуд равни на обратното съотношение на съответните стойности от различен мащаб.

И това, което е връзка обратна? Това е нищо, но обратен удар. Нашата задача е да се превърне втората съотношението да се съобрази с основното изискване на пропорциите.

Връщайки се към нашите примери и perevernom втори съотношение.

Сега пропорциите са правилни.

Ако урокът не е ясно - не се притеснявайте. Директен и обратна пропорционалност е един от конкретните теми, че хората не разбират веднага, но в крайна сметка.

В бъдеще, решаване на проблемите, вие със сигурност ще разберат тази тема. В същото време, ако имате проблеми - просто го прочетете.