Естествени числа, умножение на естествените числа и неговите свойства

Ако концертната зала се осветява от три полилеи от 25 крушки всеки, а след това всички лампи в тези полилеи ще бъде 25 + 25 + 25, т.е. 75.

Сумата, в която всички условия са равни помежду си, се записват в кратък: вместо 25 + 25 + 25 • 3 25 запис. Средните = 25 • 3 75 (фиг. 43). Броят 75 се нарича продукта от цифрите 25 и 3, и цифрите 25 и 3 наречени мултипликатори.

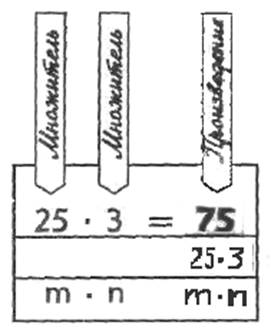
Фиг. 43. Продуктът от цифрите 25 и 3

Увеличи броя м от физическо число п - средствата за намиране на сумата от п условия, всеки от които е равна на м.

Експресия на m • п и стойността на този израз се нарича proizvedeniemchiselmin. Номерата, които се размножават наричат ​​фактори. Т.е. m и п - множители.

Съставите 4 и 7 • 4 • 7 са равни на същия брой 28 (фиг. 44).

Фиг. 44. Продуктът от 7 • 4 • 4 = 7

1. Продуктът един от двата номера не се променя, когато на пермутация множители.

Това се нарича комутативен собственост на умножение. С помощта на неговите писма, написани като:

Продукт (5 3 •) • 2 • 2 = 15 и 5 • (3 • 2) = 5 • 6 имат същата стойност на 30. След това, 5 • (3 • 2) = (5 • 3) 2 • ( Фиг. 45).

Фиг. 45. Продуктът (5 • 3) • 5 = 2 • (3 • 2)

2. За да увеличи броя на произведението на две числа, можете първо да го умножете по първия множител, а след това полученият продукт се умножава по втория фактор.

Това се нарича асоциативна собственост на умножение. С помощта на неговите писма, написани като:

Сума п условия, всеки от които е 1, е равен на п. Ето защо, равенството 1 • п = п.

Сума п отношение, всяка от които е нула, е равно на нула. Поради това равенство 0 • п = 0.

Комутативност на умножение е вярно за п = 1 и п = 0, при условие, че м • 1 = m и m • 0 = 0.

обикновено не пиша знака за умножение пред буквални фактори: вместо 8 х • 8x писмена форма. • б вместо писмен аб.

Пропуснете знака за умножение и преди скобите. Например, вместо на 2 • (а + б) напишете 2 (а + б). но вместо (х + 2) • (Y + 3) записване (х + 2) (Y + 3).

Вместо (аб) да пише ABC.

Когато записвате произведения скобите не, умножение се извършва по ред от ляво на дясно.

Прочетете произведения, като се обадите на всеки фактор в родителен падеж. Например:

1) 175 • 60 - продукт на сто седемдесет и пет и шестдесет;

2) 80 • (х 1 7) - продукт на RP RP

осемдесет и сумата на х и седемнадесет

Колко трицифрени числа (фиг. 46) може да се състои от цифри 2, 4, 6, 8, ако номерата в номерата на запис не се повтарят?

Първата цифра може да бъде всеки брой от четири цифри от данни, а вторият - всеки един от останалите трима, а третият - всеки един от останалите два. Оказва се:

Фиг. 46. ​​На проблема с подготовката на трицифрени числа

Всички тези номера може да бъде 4 • 3 • 2 = 24 три цифрено число.

борда на компанията се състои от 5 души. Измежду членовете на управителния съвет, избират председател и заместник-председател. В колко много начини може да се направи?

президент на фирмата може да избере един от 5 души:

След президентът се избира, на заместник-председателя, можете да изберете някоя от четирите останали членове на управителния съвет (Фигура 47.):

Фиг. 47. На проблема с изборите

Така че, изберете президент може да бъде по пет начина, както и за всеки избран за президент четири начина за избор на заместник-председател. Следователно общият брой на начина за избор на президент и вицепрезидент на компанията е: 5 • 4 = 20 (виж фигура 47 ..).

Ние решаваме друг проблем.

От село на село Anikeeva Bol'shova четири пътища, и от село на село Bol'shova Виноградов - три пътя (фиг 48.). Колко начина да получите от Anikeeva в Виноградов Bol'shova през селото?

Фиг. 48. На проблема на пътища

Ако от точка А до точка Б, за да получите на 1-ви път, а след това да продължи пътуването си има три начина (фиг. 49).

Фиг. 49. Възможности за пътя

Точно същата логика, ние откриваме три начина да продължат пътя започнаха да се получи и втория, и третия, и четвъртия път. Така че, просто се получи 4 • 3 = 12 начина да се измъкнем от Anikeeva в Виноградов.

Ние решаваме друг проблем.

Семейство, състояща се от баба ми, баща, майка, дъщеря и син, даде 5 различни чаши. Колко начини могат да бъдат разделени в чаши между членовете на семейството?

Решение. Първият член на семейството (например баба) има 5 заведения, в следващия (нека да бъде от мъжки пол) е 4 варианта за избор. Следваща (например, майка), ще трябва да изберете от 3 чаши, следващата - от двете, последният също така получава останалата една чаша. Ние показваме тези методи в диаграмата (фиг. 50).

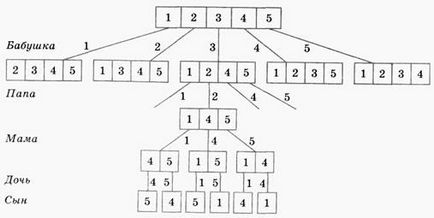
Фиг. 50. Схемата за решаване на проблема

Имаме това, което всеки избор ПЪРВЕНСТВО баба четири възможни татковци избор, т.е. само 5 • 4 начини. След Папата избра чашата, майка ми има три опции, дъщеря ми - две, синът ми - този, който е само 3 • 2 • 1 начини. И накрая, ние откриваме, че за решаване на проблема, е необходимо да откриете продукта, 5 • 4 • 3 • 2 • 1.

Имайте предвид, че получи продуктът на всички числа от 1 до 5. Тези парчета са записани в кратък:

5 • 4 • 3 • 2 • 1 = 5! (Прочетена "пет факториел").

Факторен - продуктът на всички естествени числа от 1 до това число.

По този начин, отговорът на проблема: 5! = 120, т.е. чаша между членовете на семейството може да се разпространява сто и двадесет начини.