Графичен метод за решаване на ZLP онлайн

В линейното програмиране използва графичен метод, с който се определят изпъкнали комплекти (решения многостен). Ако основният проблем на линейното програмиране е оптималният план, обективната функция заема стойност в един от върховете на разтвори многостен (вж. Фигура).

Инструкции. Изберете броя на редовете (броят на ограничения). Ако размерът на повече от две променливи, е необходимо да се въвеждат в системата, за да SZLP (см. И примери №2). Ако двойно ограничение, например, 1 ≤ x1 ≤ 4. тя е разделена на две: x1 ≥ 1. x1 ≤ 4 (т.е., броя на линиите се увеличава от 1).
Застроена площ на допустимите решения (СДТ) Можете да използвате тази услуга.

Пример на Word в

Заедно с този калкулатор също така да използвате следното:

матрица игра решение
С помощта на онлайн услуга, можете да определите цената на матрица игра (долна и горна граница), проверете точката на седлото, за да се намери решение смесени методи стратегия: Минимакс, симплекс метод, графичен (геометричен) метод, метода на Браун.

Решаването на линейно програмиране проблеми графичен метод включва следните етапи.

1. На 0X2 равнината X1 изгради директно.
2. Определена от половината равнина.
3. Определяне на многоъгълник решения;
4. Изграждане на вектор N (С1, С2), който показва посоката на обективната функция;
5. Премества обективната функция директно С1 х2 + С2 х2 = 0 в посока на вектор N в точката на многоъгълни решения.
6. Изчисляване координатна точка и стойността на целевата функция в този момент.

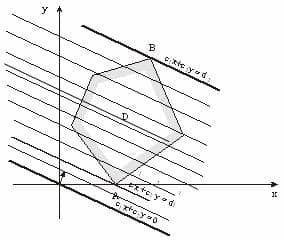
могат да възникнат следните ситуации:

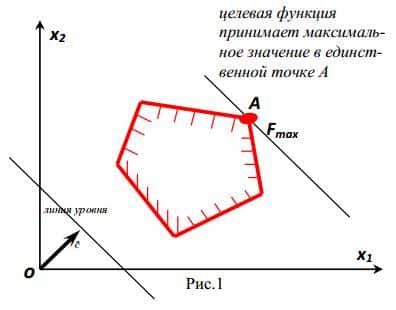
1. Обективната функция поема изключително (максимален или минимален) стойност в една точка А.
   
   
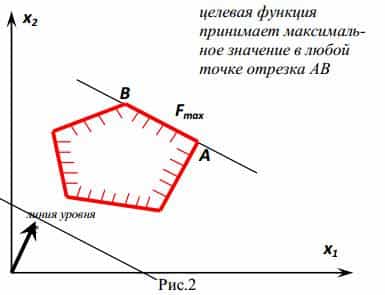
2. Обективната функция се крайната стойност във всяка точка на сегмента AB.
   
   
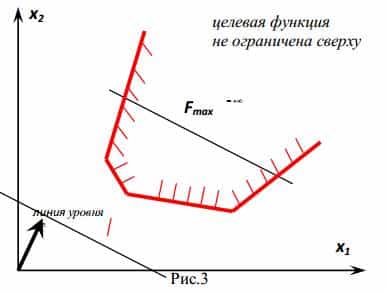
3. Целевата функция не е ограничена по-горе (при разглеждане на максимума) или по-ниска (най-малко)
   
   
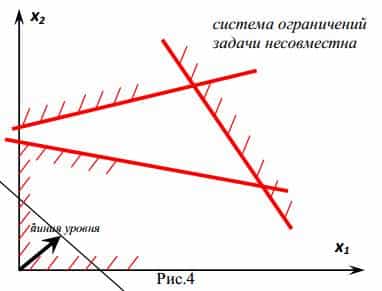
4. Системата ограничава проблемът е в противоречие
   
   

Пример. Фирмата произвежда два вида продукти - Р1 и Р2. За производство използват два вида суровина - С1 и С2. Търговия на едро единична цена е в размер на 5 CU за Р1 и 4 CU Р2. Потреблението на суровини за единица продукция тип Р1 и Р2 тип е дадена в таблицата.
Таблица - Потребление на суровини за производство

Потребление на суровини до 1 единица. продукти

Максимална опис на суровини, единици.