Графики, примери и упражнения

Графиките са възникнали през осемнадесети век, когато известната половинка-Matic, Леонард Ойлер, се опитва да се реши сега класически проблем на Кьонигсберг мостове. По това време има две Ostrova свързан със седем мостове Pregol бряга на реката и един с друг в Kenigsber-п, както е показано на фиг. 7.1. 3adacha с-в следното: извършване на разходка из града, така че, след като се мине само веднъж на всеки мост да се върне на същото място, от където започва разходката. Решаването на този проблем, Ойлер Konigsberg изобразен като графика, той се идентифицира с първите части на града, и краищата - с мостове, които са свързани с тези части. Както ние показваме в § 7.1, Ойлер успява да докаже, че от желания начин заобикаляйки града не съществува.

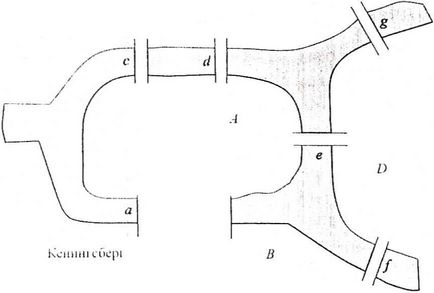
Фигура 7.1. Схема стар Кьонигсберг

В тази глава ще се въведе терминологията, която се използва в теория на графите, както и да разберат някои конкретни задачи се решават с помощта на графики. По-специално, ние гледаме на класа на графики наричат ​​дървета. Дървета - естествен модел, представляващ данните, организирани в йерархична система. Търсене на дървото за изолиране на отделни предмети и сортиране на данни в едно дърво е основна фокусна точка по компютърни науки. Допълнението към тази глава ще се справят сортиране и търсене на данни, организирани в дървета.

Фиг. 7.1 показва седем Königsberg мостове така. те са били разположени през осемнадесети век. Проблемът, към който obpa-tilsya Ойлер, въпросът е: Можем ли да намерим пешеходния маршрут, ко-торите работи само веднъж на всеки един от мостовете и започва и завършва в едно и също място в града?

модел задача - графика, състояща се от множество пикове и множество ръбове свързващи върховете. Върховете A, B, C и D символизират брега на реката и островите, а ръбовете А, А. С, D, Е и Ж означават седем мостове (вж. фиг. 7.2). Вие маршрута (ако има такъв) съответства на една верига краища на графиката, така че всеки от тях се предава само по веднъж. Разширяване ребра очевидно съответства на точката на пресичане на река моста.

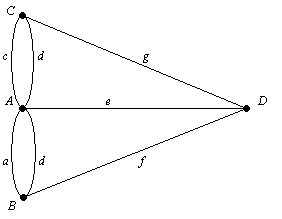
Фигура 7.2. модел на проблема с мостовете на Кьонигсберг

Графика, в който има път, има път за ранг-и завършва в същото връх и се простира до всички краища на графиката точно веднъж се нарича zylerovym графика. гума Sequence-вер (може би с повторения), през който преминава на ISCO-ми път като маршрутът самата се нарича eylerovymtsiklom. Ойлер се отбележи, че ако графиката е с цикъл на Ойлер, а след това за всеки ръб, което води до някои връх трябва да намери всеки ръб се започне от върха 1 и получени от този прост nablyudsniya това заключение: ако тази колона съществува цикъл на Ойлер след това на всеки връх трябва да бъде подходяща дори няколко ръбове.

В допълнение, Ойлер е в състояние да докаже срещу твърдението, представяния, така че графиката в която всеки чифт върховете е свързан не-последователност на ръбове е Ойлер ако и само ако всички върхове са дори степен. Степента на връх V е номер делта (V) ребрата, той intsidentnyh2.

Сега е ясно, че графиката моделиране на проблема с мостовете на Кьонигсберг, Ойлер цикъл не може да бъде намерен. Всъщност, но степента на върховете са нечетен: δ (B) = δ (C) = δ (D) = 3, и δ (A) = 5. лесно графики Ойлер ръка, подобно на това, което сме изследвани за решаване на проблема на мостове, стомана употреба- в решаването на много практически проблеми и тяхното обучение е нараснал до значително област на математиката.

Обикновено графика се определя като двойка G = (V, E), където V - ограничен набор от върховете и Е - ограничен набор от ребра, отколкото може да съдържа-вериги (ръбове, които започват и Zakan-разли- един връх) и множествена ребра (наречен многократно vayutsya множество ръбове свързващи същата двойка върхове). Графиката е показано на фиг. 7.2. Не е лесно, тъй като, например, върховете А и В са свързани с две ребра (само тези ръбове се наричат ​​множество).

Два върха ф и зеленчуците в една проста графика, се наричат ​​съседни. ако те са свързани с някои ръб напр., за които се казва, че инцидент на върха ф (и обем). По този начин, ние можем Representat-vlyat настроен Е на ръбове като набор от двойки съседни върха, като по този начин определянето нерефлексивно симетрична връзка на V. Липсата на възвратен дължи на факта, че по прост графика все още няма линии, Т. Е. Reber, двата края които са в една и съща върха. Симетрията на връзката произтича от факта, че ръб напр. Свързване на горната и V, V и се свързва с и (с други думи, ребрата не са ориентирани, че е. Е. Не се посока). Ръба само една проста графика, която свързва чифт върховете U и V, ние означаваме как и V (или вулгарис).

Logic матрица отношенията на снимачната площадка на върха, определено kotopoe ръбовете му, наречена близост матрица. Симетрията на отношенията от гледна точка на матрицата на съседство M OZNA-chaet, че М е симетрична спрямо главния диагонал. И тъй като на не-рефлексивността на тази връзка на главния диагонал на матрицата М стои символ "L".

Пример 7.1. Равен графика G (V, E) с множеството от върховете V = и ръб набор Е =. Напишете съседството матрица.

Решение. Графика G е показано на фиг. 7.3.

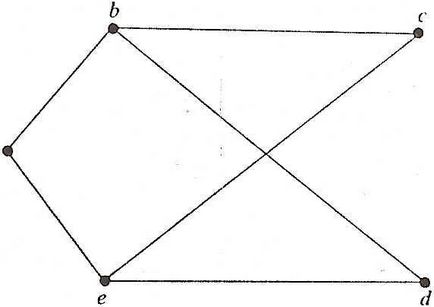
Съседството матрица е в следния формат:

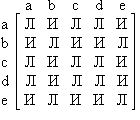
За възстановяване на графиката имаме само елементите на матрицата на съседство, които стоят над главния диагонал.

Подграф на G = (V, E) е графиката G '= (V, E), където Е "С Е V и" С V.

Пример 7.2: намери графики между Н, К и L, показано на фиг. 7.4 подграфи на G.

Решение. Означаваме върховете на графика, G, Н и К, както е показано на фиг. 7.5. Графики на H и K - подграфи на G, както се вижда от нашата нотация. Ърл L не е подграф на G, защото е на върха на индекса 4, и графиката G няма такава.

Фигура 7.9. Пример на Hamiltonian графика

Решение. Да предположим, че в един свързан граф намери Hamiltonian цикъл. Всеки връх V е включено в Hamiltonian цикъл С избора на два ръба инцидент с него, и следователно степента на всеки връх в Hamiltonian цикъл (след отстраняване на излишните ръбове) е равно на 2. Степента на върховете на графиката - 2 или 3. върховете на степен 2 включва пръстен заедно с както за инциденти с тях ребра. Следователно краищата аб, ​​ае, CD, СВ, Hi, Hg ий и в даден ред включва Hamiltonian цикъл C (вж. Фиг. 7.10.).

Bf ребро не може да бъде част от цикъла S. тъй като всеки връх на цикъла трябва да има степен на 2. Така, ребрата и Fi FG трябва да влиза в една линия С до включват връх F. Но тогава ребрата и JE GD не може да принадлежат към S. цикъл, тъй като в противен случай тя ще бъде върховете на степен три. Това ни принуждава да се включи в изданието на ребро цикъл. което води до противоречие: ребрата, бяхме принудени да избират форма две несвързани цикли вместо един, за съществуването на които сме очаквали. Заключение: Графиката е показано на фигура 7.10, не е Hamiltonian.

Hamiltonian графики се използват за моделиране на много практически проблеми. В основата на всички тези проблеми е класически проблем пътуващ търговец.

Salesman трябва да обиколите града и обратно, като са пребивавали във всеки град само веднъж, като в същото време намаляване на разходите за пътуване до минимум.

Фигура 7.10. Ребрата са включени в Hamiltonian цикъл С

Графичен модел на проблема с пътуващ търговец е Hamiltonian графика, чиито върхове представляват града и ръбовете на пътя, които ги свързват. В допълнение, всеки край е снабден с тегло посочват необходимите да се движи по подходящ начин разходите за транспорт, като, например, разстоянието между градовете или по време на шофиране на пътя 2. За да се реши този проблем, трябва да се намери Hamiltonian цикъл на минимална обща маса.

най-близкия съсед алгоритъм.

Този алгоритъм произвежда подоптимална разтвор TSP генериране Hamiltonian цикли в заредена колона с множество върхове V. Цикълът резултат от работата на алгоритъм, ще съвпадне с крайната стойност на променливата пътя, и общата дължина - крайната стойност на променливата W.

whileostayutsya сам vershinydo

Изберете сам vershinuu,

В резултат на това, алгоритъмът е намерено Хамилтън DCABD общо тегло на линия 24. Осъществяване и изчерпателно търсене на всички цикли в тази малка кутия, можете да намерите други двама Hamiltonian цикъл: ABCDA общо тегло от 23 и общо тегло от ACBDA 31. Пълният графиката с двадесет върхове съществуват около 6 1 10 16 Хамилтън цикли, прехвърлянето на които се изисква много време и паметта на компютъра.

Както вече бе споменато, е клас на графики, наречени дървета, които са особено широко използвани в компютърните приложения. Графика G = (V, E) се нарича дърво. ако тя е свързана и ациклични (т.е.. не съдържа цикли).

Нека G = (V, E) - граф КН върхове и м ръбове. Възможно е да се формулират редица необходими и достатъчни условия по kotoryhGyavlyaetsya дърво:

Всяка двойка върхове в Gsoedinena само начин.

Gsvyazen и отстраняване на поне едно от ребрата му нарушава свързаност на графиката.

Gatsiklichen, но ако добавите поне един ръб, а след това vGpoyavitsya цикъл.

Равностойността на по-голямата част от тези условия са определени лесно. Най-трудно да се справят с втория от тях. В следващия пример, ние показваме, че едно дърво с N върха има точно n-1 ръбове.

Пример 7.7. Докаже чрез индукция на броя на върховете че derevaT върхове и m КН ребра отговаря на равенство: m = n-1.

Решение. Тъй като дървото с един връх не съдържа краища, след това твърдение е вярно за N = 1.

Да разгледаме дърво T КН върховете (ръбове и т), където п> 1 и да приемем, че всеки дърво с к

Премахване на ръба на Т. трета derevoT на имот след тази процедура ще се превърне в изключен графика. Вземи точно две свързани компоненти, никой от които все още няма цикли (в противен случай, оригиналният присадката ще съдържа твърде цикли и не би могло да бъде едно дърво). По този начин, свързани компоненти - същите дърветата.

Чрез индуциране хипотеза дърво Т1 imeetn1 - 1 ребро АТ2-n2 - 1. Следователно, изходният derevoT използва (като се има предвид едно дистанционно)

Лесно е да се докаже, че който и да е свързан граф има подграф, който е едно дърво. Подграф на G. Това е едно дърво, и включва всички vershinyG. nazyvaetsyaostovnym дърво. Spanning дърво в grafeGstroitsya прост: изберете произволна ръб и последователно да се добавят другите краища, без да се създава цикъл, стига да не се добавят каквито ръбове, без да в този цикъл. Благодарение на примера 7.7, ние знаем, че за да се изгради обхваща дърво в izn графиката пикове трябва да изберете rovnon - 1 край.

Пример 7.8. Намерете две различни обхващаща дърво в чакъла, показано на фиг. 7.12.

Фигура 7.12. Свързана графика G

Решение. На тази графика, има няколко, обхващащи дървета. Един от тях се получава чрез последователно избор на ръбове: А, В, D, както е. Други - Ь, с, е и ж. Наричат ​​дървета са показани на фигура 7.13.

Методът, описан в Пример 7.8, могат да бъдат адаптирани за кратки задачи решения съединения:

Имаме нужда за изграждане на железопътна мрежа, която свързва няколко града. Известен разходи за строителство на пътища отсечката между всяка двойка градове. Задължително да се намери минималната мрежа цена.

На езика на теория на графите, ние трябва да намерим зареден графика обхваща дърво на най-малкия общото тегло. Такова дърво се нарича минималната обхваща дървото, или за по-кратко MOD. За разлика от проблема с пътуващ търговец, не е ефективен алгоритъм, който намира наистина минималната обхваща дървото. Тя е подобна на алгоритъма Prima.

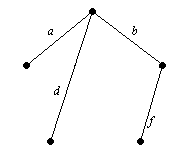
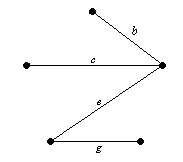
Фигура 7.13. Spanning дървета от G

алгоритъм за търсене минимум обхващаща дърво. Нека G = (V, E) - свързан претеглена графика. MOD алгоритъм изгражда графика G от избора на най-ниската възможна тегло ръбове да образуват обхваща дърво. MOD се съхранява в паметта на компютъра като множество Т ръбове.

д: = ребро grafaGs малката тегло;

Решение. Ребрата са избрани както следва: Първо - 1 DE 2 тегловни; вторият - AC тегло 3; третата - теглото на CE 7. На този етап в процес на изграждане дърво изглежда като на фиг. 7.14

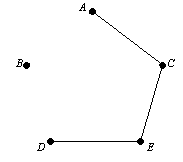
Фигура 7.14. Дървовиден изглед след три стъпки

Трябва да бъде окачена на ребро - АД, AE и CD, всяка от които е с тегло 9. Въпреки това, в зависимост от тях ние не сте добавили, завъртете цикъл. Поради изброените ребра трябва да бъдат изключени от наличните за строеж. На следващо място са слънчевите ребрата и теглото BD 11. Можете да прикачите някоя от тях, докато получават две различни MOD: тегло или 23 всеки.

Често, ние бихме искали да има дървета, които се основават на естественото образуване на йерархични структури, като, например, родословно дърво (ris.7.15). Тя показва, някои от членовете на семейството на Бернули, всеки от които е известен швейцарски математик.

А родословно дърво може да се представи по-компактно. Схемата на фигура 7.16 е пример на така наречените дърво с корен. Дърво с корен е дърво с изискан връх. Именно този специален връх и е в основата на дървото. Най-горе на дървото, лежи непосредствено под корен, се наричат ​​синове. От друга страна, най-високо, застанал точно пред сина си, наречен баща си.