Извивката и радиусът на кривината

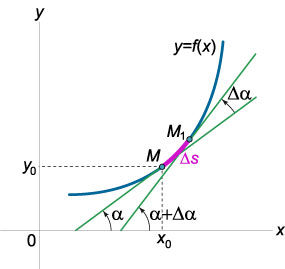
Да разгледаме кривата на равнината, определена от уравнение \ (у = F \ наляво (х \ дясно). \) Да предположим, че в точка \ (M \ наляво (\ дясно) \) проведе допирателна към тази крива, която образува ъгъл \ (\ а \) с хоризонтална ос (Фигура \ (1 \)). В изместване \ (\ Delta и \) по дължината на дъга на точка крива \ (М \) се премести да посоча \ (\) Позицията на тангента също е променен. На ъгъла на наклона на допирателната към ос \ (Ox \) в точка \ (\) ще бъде \ (\ алфа + \ Delta \ а. \) Следователно, когато (\ Delta S \) преместване на точката на кривата разстояние \ допирателна на върти \ (\ Delta \ а. \) (ще приемем, че ъгъл \ ( \ а \) се увеличава с часовниковата стрелка въртене.)

Абсолютната стойност на съотношението \ на (\ голям \ Frac >> \ normalsize \) се нарича средната кривина на дъга \ (М. \) В ограничение, с \ (\ Delta S \ 0 \), ние получаваме кривината на кривата в точка \ (М: \) \ [K = \ Лим \ limits_ \ лява | >>> \ прав. | \] от това определение следва, че кривината във всяка точка на кривата характеризира скоростта на въртене на допирателната в този момент.

За равнина крива \ (у = F \ наляво (х \ дясно) \) кривина в точка \ (M \ наляво (\ дясно) \) се изразява чрез първата и втората производни от функция \ (е \ лявата (х \ дясно) \) формула \ [K = \ Frac \ полето | >> \ дясно)> ^ 2 >> \ полето]> ^ \ normalsize >>>> \] Ако кривата е даден в параметрични уравнения на форма \ (X = х \ наляво (. т \ полето), \) \ (Y = Y \ наляво (т \ полето), \) е кривината при всяка точка \ (M \ наляво (\ дясно) \) е равна на \ [K = \ Frac \ полето |> > \ дясно)> ^ 2> + \ дясно)> ^ 2 >> \ полето]> ^ \ normalsize >>>>. \], ако кривата се дава полярен уравнение \ (R = R \ наляво (\ тета \ вдясно), \) кривината се дава от \ [+ 2 \ дясно)> ^ 2> К = \ Фрак - RR ''> \ дясна | >> + \ дясно)> ^ 2 >> \ прав]> ^ \ normalsize . \] радиусът на кривината на кривата в точка \ (M \ наляво (\ дясно) \) >>>> се нарича обратна извивка \ (К \) дава крива при дадена точка: [. R = \ Frac \] \ Следователно равнинни криви дадени изрично уравнение \ (у = F \ наляво (х \ полето), \) радиус кривина в точка \ (M \ наляво (\ дясно) \) се дава с израза \ [R = \ Frac \ дясно)> ^ 2 >> \ полето]> ^ \ normalsize >>>> \ полето | >> \].

Изчислява кривината на елипса \ [\ Frac >>>> + \ Frac >>>> = 1 \], в своите върхове.

Очевидно е, че е достатъчно да се намери кривината елипса в точки \ (А \ наляво (\ дясно) \) и \ (B \ наляво (\ дясно) \) (Фигура \ (2 \)), тъй като поради симетрията на кривината на крива в два противоположни върха елипса ще бъде същото.

За изчисляване на кривината е удобно да се движат от елипса канонично уравнение на уравнението в параметрична форма. \ [X = а \ защото т, \; \; \; у = б \ грях т \.] Когато \ (т \) - параметър. В точка \ (А \ наляво (\ дясно) \) параметър е настроен на \ (т = 0, \) и в точка \ (B \ наляво (\ дясно) \) стойността му е \ (т = \ голям \ Frac \ normalsize. \)

Намери кривината и радиусът на кривината на парабола \ (у = \) в основата.

Намери кривината и радиуса на кривината на кривата \ (у = \ защото х \) при максималната точка.

Тази функция достига максимум в точките \ (х = \ голям \ Frac> \ normalsize \ п \ в Z. \) С периодичността на кривината във всички точки идентичен максималните, така че е достатъчно да се разглежда само точка \ (х = 0 \).