Как да се изчисли дължината на диагонала на квадрата

Диагонала на квадрата - сегмент, който свързва противоположните краища на квадрат и преминава през центъра му. За изчисляване на диагонала на квадрат, използвайте формула D = S 2 >>. където е - страната на квадрата. Задачите трябва да намери диагонала на квадрата на настоящата стойност на друго количество, като по периметъра или поле. В тези случаи е необходимо да се използват и други формули за изчисляване на първата част на площада, а след това - на диагонала.

стъпки Редактиране

Метод 1 от 3:
Изчисление на диагонала на квадрат на известен цитат

Да се ​​намери дължината на площада. Най-вероятно, дължината на площада ще бъде даден в проблема. Ако работите с истински обект, измерване на негова страна с линийка или шивашки метър. От площада всички страни са равни, мярка или намери дължината на всяка страна. Ако квадратен дължина страна не е известно, този метод не може да се използва.

• Например, даден квадрат със страни на 5 cm.

Запис формула г = S 2 >>. В тази формула, г - диагонала на квадрат, S - страната на квадрата. [1]

• Тази формула е получена от Питагоровата теорема (2 + 2 б = C 2) + б ^ = C ^)>. Диагонала квадратен разделя на две равни правоъгълен триъгълник, т.е. частта от квадрата може да се използва за изчисляване на диагонала на квадрата, който е хипотенузата на правоъгълен триъгълник.

Формулата за заместване на стойността на дължината на страната на квадрата. Това означава, че тази стойност трябва да се замести с.

• Например, ако един квадратен страна е 5 см, формулата се записва, както следва:
  г = 2 май >>

Умножете страна на площада в 2 >>. да се намери диагонала на квадрата. Изчисление изпълняват по-добре на калкулатора, за да получите точен отговор. Ако не разполагате с калкулатор, 2 кръг >> до 1414.

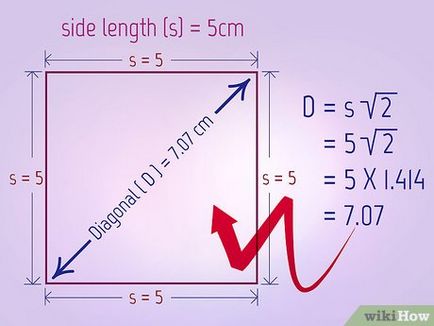
• Например, ако един квадратен страна е 5 см, формулата може да се запише като
  г = 2 май >>
  г = 7. 07
  Така диагонала на квадрат е равно на 7.07 cm.