Как да се изгради една парабола

Уравнения с учебната програма решаващи са учениците в клас 6-7, но такива примери ги придружават по-късно навсякъде. Особено трудно е дал на децата за изграждане на геометрични характеристики на изображението, и затова ще научите в тази статия за това как да се изгради парабола - графика на квадратното уравнение, това, което по същество е. Постройте парабола на окото е трудно, но ако следвате тези прости съвети от статията и да научите как да направите това в клас, няма да бъдат равни.

Координира самолет. Параболата е изграден от три точки, и това е защо ние трябва да построим координатна равнина. Две перпендикулярни оси х и у ще бъдат ръководството, и ученикът трябва да просто изберете размера на единица интервал. Обикновено това е една клетка в тетрадка, но може да предприеме всякакви други удобно за вас znachchenie. Да се ​​изгради парабола чист и гладък, всички точки, трябва да се поставят точно на линията, в противен случай програмата ще "мръсни" и би било трудно да се чете или да се използва като решение на уравнението, например.

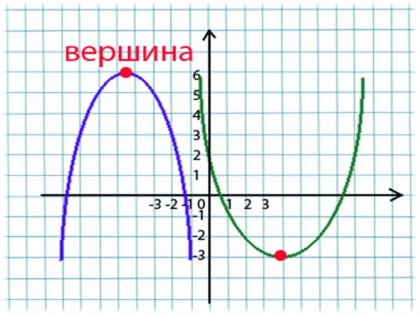
Върхът на параболата. Стандартният квадратно уравнение има формата:

За да се построи парабола, е необходимо да се започне да се изчисли местоположението на върха на него, и от която ще тръгне нагоре или надолу, за графика клонове. За да направите това, използвайте следната формула:

Вижда се, че в уравнение х - координиране на върха по хоризонталната ос, а А и Б - цифри, които се вземат от оригиналния уравнението. За да намерите координатите на върховете на оста у е достатъчно просто да се замени стойността намерен в квадратно уравнение оригинален х.

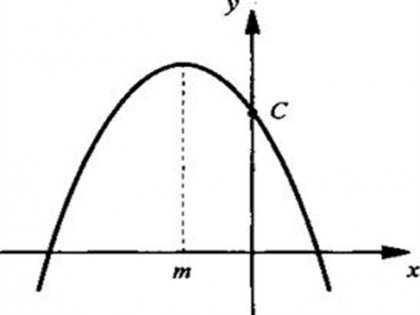
Клон на параболата. Постройте парабола - средство за решаване на квадратно уравнение, и че отговорът ще бъде вярно само ако функцията е изградена перфектно. За да направите това, вие трябва да помисли за още един параметър - по посока на клоните на параболата, която определя дали то се увеличава или намалява. Да се ​​изгради парабола правилно, трябва да прочетете това квадратно уравнение:

парабола посока е коефициентът на променливата във втората степен. Ако броят на положителните и - функция увеличава, насочена нагоре; ако отрицателен - намаляване надолу.

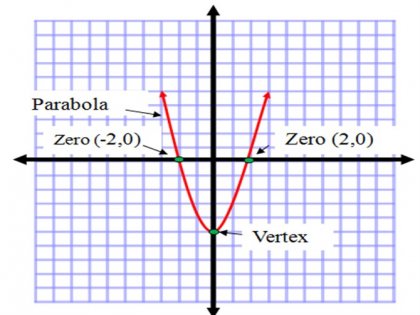
Нули. За да разберете местата, където параболата пресича оста х, е необходимо да се намери нули. Може да се направи това, като се равнява на оригиналния квадратно уравнение на нула, т.е. необходимостта от подмяна на параметъра в 0. Тези корени са координатите на пресечната точка на парабола ос х. Съответните координатите по оста у е 0.

Важно! Преди да се изгради парабола Начертайте вертикална пунктирана линия, перпендикулярна на оста х, върху която е на върха: това е необходимо да се гарантира, че една от страните функции имат друг симетричен.

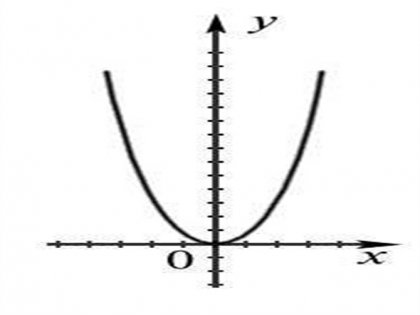
Стойностите на функцията. Сега най-важното: как да намерите на стойностите на функцията, за да се изгради правилно парабола? Необходимо е да се произволно да отнеме няколко положителни и отрицателни числа, като ги замени с квадратно уравнение за променливата и поръчате получената цифра. По този начин, броят на избраните студенти - стойността на х. чрез заместване на получената стойност - ос у. Намерете ги в самолета координира и леко извита линия на поведение парабола. Готово!

14512 14513 14514 14515 14516

За да се построи парабола, чрез скалата, както и разгледа няколко важни фактора:

• Влезте четвърт от координатната равнина. Съветът е много полезно при определяне на знака за решаване на квадратно уравнение
• Изграждане на масата. Начертайте малка маса, която ще донесе на стойностите на х и у в процеса на изчисление: така че да не се объркват и да си свършат работата както трябва.