Как да се намери периметъра на шестоъгълника

За да намерите по периметъра на шестоъгълника. измери и да добавите до дължините на всички свои шест страни. P = А1 + А2 + A3 + A4 + A5 + a6 където Р - периметър на шестоъгълника. и А1, А2, ... a6 - дължината на своята storon.Edinitsy измерване на всяка от страните, са от един и същи вид - в този случай, би било достатъчно, за да се установят само числови стойности на дължините на страните. Мерната единица на периметъра на шестоъгълника ще съвпадне с двете страни на устройството.

Primer.Imeetsya шестоъгълник със странични дължина 1 cm, 2 тМ, 3 мм, 4 mm, 5 mm, 6 мм. Вие искате да го намерите perimetr.Reshenie.1. Единица за измерване на първата страна (см) се различава от дължини на другите страни на мерните единици (мм). Ето защо, преминете на 1 см = 10 mm.2. 10 + 2 + 3 + 4 + 5 + 6 = 30 (mm).

Ако шестоъгълника е вярна, тогава да се намери периметъра, умножете дължината на страните му в шест: P = A * 6, когато - дължината на страните на правилен шестоъгълник .Primer.Nayti периметър на правилен шестоъгълник с дължина на страната 10 sm.Reshenie: 10 * 6 = 60 (см).

Правилен шестоъгълник има уникална функция: радиуса на окръжността около такова шестоъгълник равна на дължината на страните му. Ето защо, ако радиусът на кръга е известно, да се използва формулата: Р = R * 6, където R - радиус на окръжност кръг.

Primer.Rasschitat периметър на правилен шестоъгълник. пише в кръг с диаметър от 20 sm.Reshenie. Радиусът на описаните окръжности ще бъде равен на: 20/2 = 10 (см) .Sledovatelno периметър шестоъгълник. 10 * 6 = 60 (см).

Ако условията на задачи, посочени радиус на вписан кръг, след това се прилага формулата: Р = 4 * √3 * R, където R - радиусът на вписан кръг на правилен шестоъгълник.

Ако знаете, че площта на правилен шестоъгълник. след това да се изчисли периметъра, използвайте следната връзка: S = 3/2 * √3 * ² където S - площ на правилен шестоъгълник. Следователно е възможно да се намери = √ (2/3 * S / √3), като по този начин: P = а = 6 * 6 * √ (2/3 * S / √3) = √ (24 * S / √3) = √ (8 * √3 * S) = 2√ (2S√3).

Според определението на планиметрия правилен многоъгълник се нарича изпъкнал многоъгълник, чиито страни са равни и ъглите като равни. Правилен шестоъгълник е правилен многоъгълник, с редица страни, равна на шест. Има няколко формули за изчисляване на площта на правилен многоъгълник.

Ако известно радиуса на кръга, описан около многоъгълника, повърхността може да бъде изчислена по формулата:

S = (N / 2) • • R² грях (2π / N), където N - броят на страните на многоъгълника, R - радиусът на кръга, π = 180 °.

Във всички краища на правилен шестоъгълник са 120 °, така че формулата ще бъде:

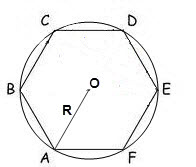
В случая, когато окръжност с радиус R вписан в многоъгълника, площ се изчислява по формулата:

S = N * r² * TG (π / N), където N - броят на страните на многоъгълника, г - радиусът на вписан кръг, π = 180 °.

За шестоъгълник, тази формула е под формата:

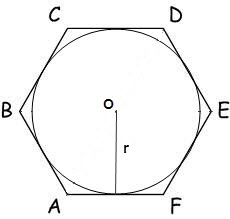
Площта на правилен многоъгълник също може да бъде изчислена, като знаем само от дължината на страните му по формулата:

S = п / 4 * ² * CTG (π / п), п - брой страни на многоъгълник, а - дължина на страната на многоъгълника, π = 180 °.

Съответно, областта на шестоъгълника е:

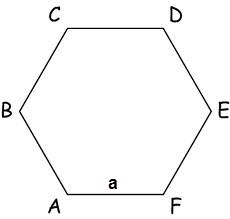
• шестогранници площ формула

Проблемите с геометрия често се налага да се намери perimetrfigury. Периметърът на фигурата е дължината ограничава неговата линия. Можете, разбира се, просто се измери дължината на линията. Въпреки това, резултатите от тези измервания може да не са достатъчно точни. Освен това, измерването на дължината на кривата - доста труден процес. Ето защо, на практика и в решаването на геометрични проблеми обикновено се използва специална формула.

• владетел, компас, калкулатор

За да намерите perimetrfigury. Ограничен с прекъсната линия, добавете дължините на всички негови съставни сегменти. Ако дължините на сегментите не са известни, се измери това с линийка и компас. Ако формата е с относително голям размер, използвайте лента мярка. Единицата за Границите и ще служи същите единици, които са определени (измерена) дължина на сегментите на компоненти. Ако единици са различни, те трябва да се намали до една vidu.Naprimer, ако земята е с триъгълна форма със странични дължини от 10, 20 и 30 метра, съответно, тогава периметъра е: 10 + 20 + 30 (m).

За да намерите периметъра на прости геометрични фигури, използвайте специален търсене formulami.Chtoby периметър ромб (по-специално, на квадрат), тя се умножава по дължина четири страна. Това означава, че се използва следната формула: Р (диамант) = P (квадрат) = 4 * S,
където - ромб дължина страна (квадратчета), L - своя периметър.

За периметъра на успоредник (по-специално, правоъгълник), се добавя на дължината и ширината и се умножава по две (с дължина и ширина се отнася до дължината на две съседни страни). Графично, това може да се запише, както следва: Р (успоредник) = Р (правоъгълник) = 2 * (D + w), където:
и w г - дължината и ширината на успоредник (правоъгълник), съответно.

За да намерите по периметъра на кръга, изчисли дължината на окръжността ограничаващата рамка. За това се използва класически формула: R (кръгче) = π * D или
P (кръгче) = 2 * π * F
където: D - диаметър на кръга, R - радиусът на кръга, π - брой "пи", приблизително равна на 3,14.

Ако знаете, че дължината на диагонала на квадрата, а след това да се намери периметъра и да използвате следната формула: P (квадрат) = 2√2 * г, където г - дължината на диагонала на квадрата.

Периметърът на площада може да се изчисли като се използва информация за своята област. За тази цел се използва следното правило: P (квадрат) = 4 * √Skv където SKV - квадратни.

Perimetrommnogougolnika нарича затворена начупена линия, състояща се от всичките си страни. Търсенето на този параметър намалява дължината на сумиране на дължините на страни. Ако всички сегменти, формиращи периметъра на двуизмерен геометрични фигури са със същия размер, многоъгълника се нарича редовно. В този случай, изчисляването на периметъра е значително опростена.

В най-простия случай, когато известен страничен дължината (а) на правилен многоъгълник, а броят на възли (н) в него, за да се изчисли дължината на периметъра (Р), просто се размножават тези две стойности: P = A * п. Например, един правилен шестоъгълник с дължина страна на периметъра на 15 см трябва да бъде равен на 15 * 6 = 90 cm.

Изчислява периметъра на такъв многоъгълник чрез известен радиус (R), описани в кръг около него също е възможно. За това е необходимо да се изрази дължината на първата странична използване на радиуса и броят на върховете (п), и след това се умножава получената стойност на броя страни. За да се изчисли страна дължината на радиуса размножават синуса на пи, разделен на броя на възлите и удвояване на резултата: R * грях (π / п) * 2. Ако предпочитате да се изчисли тригонометрични функции в градуси, сменете пи 180 °: R * грях (180 ° / о) * 2. Периметър изчисляване на стойността, получена чрез умножаване на броя на върховете P = R * грях (π / п) * 2 * п = R * грях (180 ° / о) * 2 * п. Например, ако шестоъгълник вписан в окръжност с радиус от 50 cm, периметъра ще има дължина 50 * грях (180 ° / 6) * 2 * 6 = 50 * 0,5 * 12 = 300 cm.

По подобен начин е възможно да се изчисли периметър, без да знае дължината на страната на правилен многоъгълник. ако е описано за кръг с известен радиус (R). В този случай, формулата за изчисляване на размера на фигурата ще бъде различен от предишния само поддръжка за тригонометрични функции. Промени във формулата за задължително допирателната да се получи експресия: R * TG (π / п) * 2. Или за изчисления в градуси: R * TG (180 ° / о) * 2. За да се изчисли периметъра увеличаване на стойността, получена в редица пъти, колкото е броят на полигон върхове. R = R * TG (π / п) * 2 * п = R * TG (180 ° / о) * 2 * п. Например, осмоъгълна периметър описано следващия кръг с радиус от 40 cm, ще бъде приблизително равна на 40 * TG (180 ° / 8) * 2 * 8 ≈ 40 * 0.414 * 16 = 264.96 cm.

• многоъгълник периметър формула