Как да се провери дали даден номер е председател

Primes - числа, които са неделими само от себе си и 1; Всички други числа се наричат ​​съставни числа. Има много начини да се определи дали даден номер е председател. Някои методи са относително прости, но те не са подходящи за големи количества. Други методи, полезни за голям брой всъщност представляват вероятностни алгоритми, които са понякога погрешно характеризират като няколко прости или композит.

стъпки Редактиране

Метод 1 от 4:
Бюст разделители Редактиране

Бюст разделители - най-лесният начин да се определи лесното. В случай на малък брой е може би също така най-бързия начин. Тя се основава на определянето на просто число: броят е премиер, ако тя все още няма делители освен себе си и един.

Нека п - брой да бъдат тествани. При този метод, трябва да се разделят на броя н за всички възможни разделители числа. За по-големи стойности на N, например, N = 101, проверка всеки разделител отнема много време. Но има начини да се намали броя на разделители, които искате да проверите.

Преценете дали Броят п е още. Всяко четно число се дели на 2. Ако цялото число п - равномерното, а след това можете веднага да декларира, че не е проста (тоест, е неразделна номер). За бързо определяне на паритета на обърнете внимание на последната му цифра. Ако последната цифра от 2, 4, 6, 8.0, този брой е дори и да не е лесно.

• Единственото изключение от това правило - броят 2. Така е и дели само по себе си и 1, 2 броя - просто число. По този начин, номер 2 е само странно, просто число.

Разделете п за всяко цяло число от 2 до N-1. От делителя е по-малко от дивидента, проверката на всички делители по-малко от п и по-голямо от 2, трябва да покаже дали н председател. Започвате с число по-голямо от 2, защото четни числа (които са кратни на 2) не са прости числа. Това не е най-ефективният начин за тестване primality, но има няколко методи за тестване оптимизация.

• Например, вижте номер 11. В този случай, разделение (равномерно) 11 3, 4, 5, 6, 7, 8, 9, 10. Тъй като нито един от тези номера не се разделят (равномерно) 11 броя 11 - прост номер.

За да спестите време, проверете разделители за закръглена стойност на квадратен корен (н). Проверете всички делители от 2 до N-1 може да отнеме време. Например, ако искате да проверите броя на 103, тогава ще трябва да се тества следните делители: 3, 4, 5, 6, 7, и т.н. до 102! Но това може да се избегне - просто проверете разделители между 2 и заоблени квадратен корен (н).

• Обяснение на този принцип. Да разгледаме множители 100. 100 = 100 х 1, 2 х 50 4 х 25 5 х 20, 10 х 10, 20 х 5 х 25 4 2 х 50, 100 х 1. Отбележете, че след двойката множители 10 х 10 всички двойки на множители се повтарят (само фактори в тези двойки се разменят). Следователно, можете да игнорирате делителите на п е по-голямо от корен квадратен от (н).
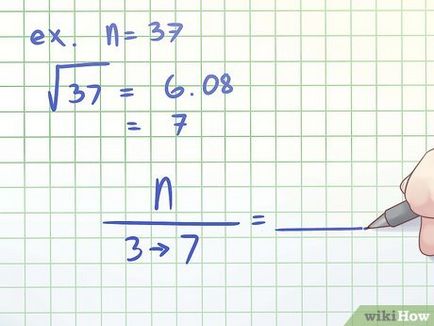
• Например, п = 37. проверка не трябва да се тества всички делителите на от 3 до 36. Вместо това, проверката разделители между 2 и закръглена стойност на корен квадратен (37).
  • На корен квадратен (37) = 6.08. Кръгла този брой до 7.
  • 37 не се дели на 3, 4, 5, 6, 7, така че - просто.

За по-нататъшно спести време, тества само председатели делители. По дефиниция, всеки композитен номер може да бъде изразено като продукт на две или повече прости числа. Поради това разделение Броят п за неразделна разделител - излишно операция се повтаря разделение на п в председатели делители. По този начин, можете допълнително да ограничите тест серия разделители на.

• Това означава, че всички, дори делители и всички делители на които са кратни на простите числа могат да бъдат пропуснати.
• Например, вижте номер 103. корен квадратен от 103 се закръгля до 11. Обикновено разделители 2 до 11 е 3, 5, 7, 11. Разделители 4, 6, 8, 9, 10 може да бъдат пропуснати (9 кратни на 3 и всички други разделители - четни числа). По този начин можете да намали броя на тестовите разделители до четири цифри.
  • Паравани 3, 5, 7, 11, не споделят (равномерно) номер 103, така че - просто.