константа на Болцман

Boltsman Людвиг (1844-1906) - великия австрийски физик и един от основателите на молекулно-кинетичната теория. В писанията на Болцман молекулно-кинетичната теория за първи път се появява като функциониране, съгласуван физическа теория. Болцман даде статистическа интерпретация на втория закон на термодинамиката. Те направиха много за развитието и популяризирането на електромагнитното поле на теорията на Максуел. А борец от природата, Болцман пламенно защитава необходимостта молекулно тълкуване на термични явления и се тежестта на борба с доктрината, че отрича съществуването на молекули.
В уравнение (4.5.3) влиза съотношение постоянна универсален газ за постоянен R NA Авогадро. Това съотношение е еднаква за всички вещества. Тя се нарича константа на Болцман, в чест на Болцман, един от основателите на молекулно-кинетичната теория.
константа на Болцман е:
Уравнение (4.5.3) с константа на Болцман е написано, както следва:
Физическият смисъл на константата на Болцман
Исторически погледнато, температурата беше представен за първи път като термодинамична количество и мерна единица е определен за него - градуса (виж § 3.2.). След установяване на комуникация с средната температура на кинетичната енергия на молекулите стане ясно, че температурата може да се дефинира като средната кинетичната енергия на молекулите и изразяват в джаули или ерговете, т. Е. Стойности на Т вместо влизат в стойност T * така че
Така определената температура, свързани с температура, изразена в градуси, както следва:
Затова Болцман постоянна стойност може да се разглежда като свързващ температура, изразено в енергийни единици, температура, изразена в градуси.
зависимост газ под налягане от концентрацията и температурата на молекулите
Изразяване Е от (4.5.5) и заместване на формула (4.4.10), ние получаваме израз показва зависимостта на налягането на газа на концентрацията и температурата на молекулите:
Формула (4.5.6), следва, че при същите налягания и температури в концентрацията на молекули на газове е същото.
Следователно право Авогадро: равни обеми от газове при еднакви температури и налягания, същия брой молекули.
Средната кинетичната енергия на транслационно движение на молекули е пряко пропорционална на абсолютната температура. Коефициентът на пропорционалност - Boltsmanak константа = 10 -23 J / K - за запомняне.
§ 4.6. Максуел разпределение
В много случаи знанието на някои средни стойности на физични величини не е достатъчно. Например, знанието на средния план човешкия растеж не позволява освобождаването на дрехи в различни размери. Ние трябва да знаем приблизителния брой на хора, чийто ръст е в определени граници. Също така е важно да се знае броя на молекули със скорост, различна от средното. Максуел първо намери, може да се определи тези цифри.
Вероятността за случаен събитие
В §4.1 споменахме, че да се опише поведението на голяма популация от молекули J. Максуел въвежда понятието вероятност.
Както подчертават по принцип е невъзможно да се проследи изменението на скоростта (или импулс) на една молекула в продължение на дълъг период от време. Нито точно да се определи скоростта на молекулите на газа в даден момент. От макроскопска среда, в която газът е (определено количество и температура), не възниква с необходимостта от определени стойности на молекулни скорости. Speed молекула може да се разглежда като случайна променлива, в която данните на макроскопски условия могат да вземат различни стойности, като всеки брой точки от 1 до 6 (броят на лицата е шест кост) може да попадне в хвърляне на зара. Познайте колко точки попадат в тази хвърляне на зарове, не можете. Но вероятността да падне, да речем, пет точки, за да се определи.
Каква е вероятността от случайно събитие? Нека да произвежда много голям брой тестове N (N - брой на зарове хвърля). В този случай, случаи N 'настъпили благоприятен изход изпитвания (т. Е. Загуба на пет). Тогава вероятността за това събитие е съотношението на броя на случаите с благоприятен изход за пълния брой тестове, при условие, че този номер, тъй като много голям:
За симетрични кости вероятност за всеки избран брой точки от 1 до 6, равна
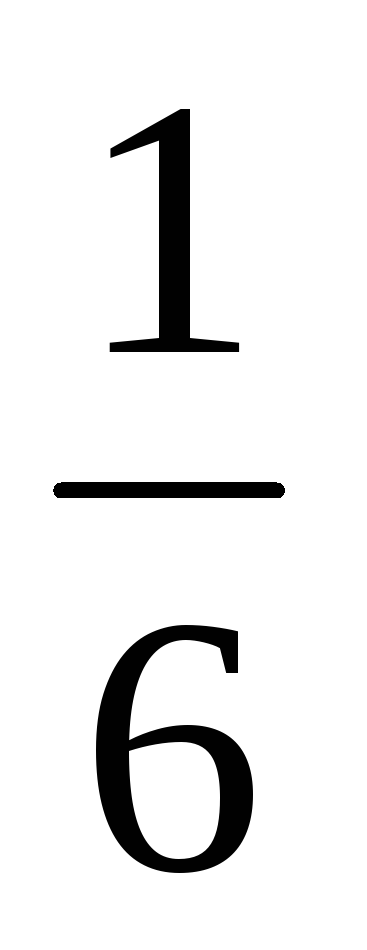
Ние виждаме, че определен количествен модел се открива на фона на поредица от случайни събития, се появява номера. Този номер - вероятността - позволява да се изчисли средно. Така че, ако направите 300 хвърля костите, средният брой на падане на пет, както следва от формулата (4.6.1), ще бъде равен на: 300 ·
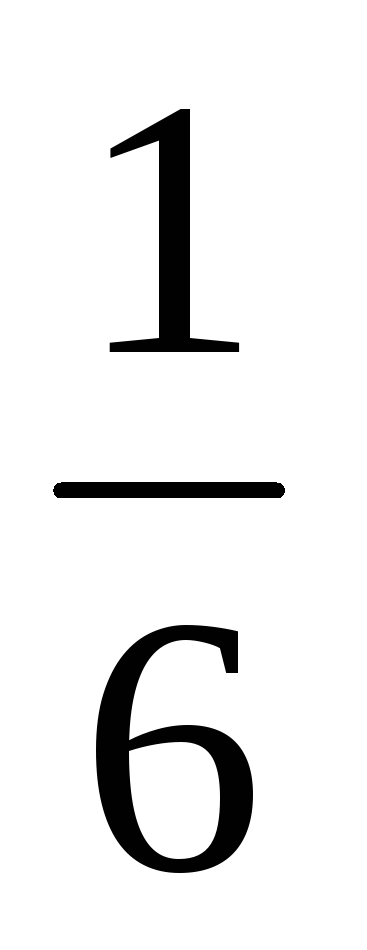
Няма съмнение, че поведението на молекулите на газа в съда е много по-сложно движение хвърлени зара. Но можете да очаквате да намерите някои количествени закони, които позволяват да се изчисли статистическата стойност, дори и само да позира на проблема, както и в теорията на игрите, а не като в класическата механика. Необходимо е да се откаже от нерешения проблем за определяне на точната стойност на скоростта на молекулата в момента и се опитайте да намерите вероятността нормата е от значение.