Методи за графика задача
В областта на математиката, много по-силен, отколкото в други дисциплини намерени черта на организацията, като се стреми да открие скрит ред във всичко, което ни заобикаля.
Съществуват различни начини за определяне на графиката: геометрични (чертежи, схеми, диаграми), прост списък на върхове и ръбове, табличен. Човекът е удобно да се работи с броенето модел, тъй като тя може лесно да се установи връзка между възлите в зрителната форма с помощта на ребра изобразени с непрекъснати линии. Такава геометрична представяне на равнинна графика се нарича неговото прилагане. При обработката на по-лесно да се определи броят на алгебрични форма - изброяване (списък) върховете или ръбовете.
Например, насочена графика на фиг. 2.3 може да се определи от двойки (V1, V2), (V2, V3), (V2, V3) и (V1, V1), което съответства на дъги (R, и Т, S). По време на прехода от алгебрични геометричен метод на една и съща графика може да съответства на различни изображения - изоморфни графики, подходящи изображения зависи, например, собственост плосък realizability. За да направите това, вие трябва да зададете правилно самият граф.
Основният начин да се уточни броят е да се изброят всичките му върхове и ръбове. Но такава цел, от една страна, асиметрично (с него е трудно да се работи с, особено компютри), и второ, да се уточни всеки ръб имате нужда от повече време, за да напише съответните върхове толкова зле по отношение на компресия и съхранение. Понякога графика дадена маса, състояща се от N реда (горе) и м колони (ребра). Основно всички методи задача графика (таблица графика матрица) е да определи съответствието между комплекта п върховете Vi и Т ръбове X I.
Един от най-разпространените начини за уточняване на графиката е методът на матрица. Да предположим, че са дадени графика G (V, X), където V = 1, V2. Vn> - върхове и X = 1, Х2 ,. Xm> - ръбове на графиката.
Ние наричаме честота матрица таблица В, състояща се от N реда (горе) и м колони (ребра), в които:
за ненасочена графика:
за насочено графика:
Очевидно е, че във всяка колона на матрицата на честота трябва да бъде само две не-нулево число, тъй като острието е инцидент с два върха. Броят на ненулеви елементи във всеки ред - степента на съответния връх. Но в областта на математиката по-лесно да се работи с квадратни матрици, а подходящи алгебрични инструменти са добре проектирани за тях.
Ние наричаме близост матрицата на графиката G (V, X) без множество ръбове квадратна матрица на за п, където:
Тъй като за ненасочена графика ръбове (Vi. Vj) и (Vj. Vi) едновременно принадлежат или не принадлежат на графиката, като символ на една и съща линия, на Aij == Aji. Матрицата на съседство на ненасочена графика е симетрично и не се променя, когато транспонират.
Въпреки че формално всеки връх винаги в непосредствена близост до себе си, в матрицата на съседство ние поставяме Aij = 0, ако тя няма контури и Aij = 1, ако има един цикъл. Така че, ако графиката е матрицата за близост и не зависят от главния диагонал винаги нули.
Например, насочена графика на фиг. 2.3 Може да се определи честотата таблица (Таблица 2.1.).
Таблица 2.1. Таблица честота диграфа
Графика с множество ръбове (особено насочено графиката) е трудно да се определи с помощта на матрица близост. Да го направим официално. Ако графиката е ненасочена, тогава имаме Aij == Aji. и е равна на множеството ребра (Vi. Vj). По-специално, ако I = к, тогава Aij - броят на бримки в Vi. Недостатъкът на този подход се състои в това, че остава в неизвестност взаимна договореност на няколко ръбове. По този начин, ребрата могат да се припокриват един с друг, което, за съжаление, не засягат матрицата близост.
Имайте предвид, че за това определяне насочен графика без успоредни ръбове на графиката е частен случай на графиката с множество ребра на всеки ръб множество равно на 1 или 0. Очевидно е, че за два върха Vi и Vj (i¹j) има две основни възможности:
Ако всички краища излизат от един към друг и включва върха
или ако за всеки връх съществува двете входящи и изходящи краища.
Нека пълната многообразието на ръбове, равни на п. докато от връх до връх Vj Vi излъчват m £ п ръбове, и на Vj Vi произхождат от N - м ребра. След това клетъчната Aij пиши м. и клетъчни Aji пишат п - м Ако има няколко линии, като всички те са свързани с един връх Vi .. Ето защо, в запис множествеността клетка AII на електрически вериги при Vi.
Такава графика задача има същите недостатъци като ориентирани, и все пак пренебрегване посоката на взаимно споразумение. Обаче, основният недостатък е, че с тази дефиниция на матрица близост (като графика с множество ръбове и без тях) не винаги е възможно да се определи чрез насочена графика близост матрица или не.
Честотата матрици няма такъв проблем, защото наличието на Форма елемент е -1 критерий ориентирани графика. За близост може да бъде достатъчно за ориентация матрица асиметрия, но не критерий. Например, графика с близост матрица може да съответства на сегмент V1 V2 на (и двете върховете) - или пръстенен ненасочена графика с две ръбове V = 1, V2); (V2, V1)> - диграфа. Тя -essential недостатък и той се появява само, когато се опитват да се определи матрицата близост за графика с множество ръбове е да се уточнят насочен граф с близост матрица (ако се окаже, симетрична) трябва или да посочите това отделно, например AOP, или който и да е елемент на матрица напише "-".
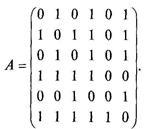
Проблем 19. Да предположим, че графиката G е дадено близост матрица A. Диаграмите на тази графика, ако
Проблем 20. Да предположим, че графиката G е дадено близост матрица A. Диаграмите на тази графика, ако
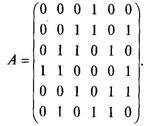
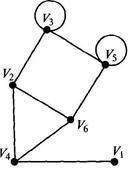
Решение. Графика графика с шест върха, ние представяме на фиг. 2.19.
Всяко насочено графика е двоичен връзка A V, където множество от върховете на V-, X- и двойки ребра.
За определен брой върхове V съотношение X могат да бъдат представени по три начина:
графично, т.е. диаграма (Фигура 2.19.);
с помощта на таблици, които са представени от един и 0;
използване матрици (в случая на съседство матрици).
Тази форма на връзката е полезен при решаването на много логични и индустриални проблеми. Тя се използва и при механична обработка да организираме информацията