Производни, както и въвеждането на определение в 10 клас по алгебра
Какво ще да научите:
1. Въведение в концепцията на производно.
2. Малко от историята.
3. Определяне на производно.
4. производно функцията на графиката. Геометрична смисъл на производно.
5. Алгоритъмът за намиране на функцията производно.
6. Разграничаване на функциите.
7. Примери.
Въведение в концепцията на производното
Има много задачи много различни по значение, но има и математически модели, които ни позволяват да разчитате на нашите цели по абсолютно същия начин. Например, ако вземем предвид такива задачи като:
а) Има известна банкова сметка, която постоянно се променя на всеки няколко дни, сумата постоянно се увеличава, то е необходимо да се намери скоростта, с която се увеличава за сметка.
б) Заводът произвежда бонбони, бонбони е постоянно увеличение на продукцията, да се намери колко бързо увеличаване на растежа на шоколадови бонбони.
в) скорост на превозното средство в определено време Т, ако е известно положение на превозното средство, и се движи по права линия.
г) Ние насрочи дадена функция и точка проведе допирателна към него, е необходимо да се намери на наклона на допирателната.
Формулирането на целите ни са доста различни, и изглежда, че те са решени напълно различни начини, но по математика, за да разбера как може да реши всички тези проблеми по абсолютно същия начин. концепцията на деривата е въведен.
Малко от историята
Терминът производно се въвежда голям математик - J. Lagrange, преведен на български език произлиза от френската дума derivee, той също така въведе модерната нотация на деривата, че ще се счита за по-късно.
Смятан понятието производна в работите Лайбниц и Нютон, нашата използването на термина те са в геометрията и механиката, съответно.
Малко по-късно ще разберем какво производно се определя от лимита, но има лек парадокс в историята на математиката. Математиците са се научили да броят производно преди въвежда понятието граница и действително да разберем това, което е производно.
определение на производно
Нека функция у = F (х) се определя на определен интервал, съдържащ в себе си точка x0. Аргумент увеличение Δx - не излизат от нашата гама. Намираме нарастване Δy и образуват съотношението Δy / Δx, ако границите на това съотношение, когато Δx клони към нула, определената граница се нарича производно с функция у = F (х) при x0 и означен F '(x0).
Нека се опитаме да обясним какво производно не е в математически термини:
В математически език: производно - граница на съотношението на функцията за увеличение на нарастване на аргумента си клони към нула нарастване на аргумента.
В обикновения език: производно - функционира степента на промяна в точка x0 на.
Нека да разгледаме графиките на три функции:

Момчета, какво мислиш, която на кривите расте по-бързо?
Отговорът изглежда е очевидно за всички 1, кривата расте по-бързо от останалите. Търсим колко готино качвах графика на функцията. С други думи - колко бързо се променя, когато промените ордината х. Една и съща функция на различни места може да има различна стойност на производното - т.е., може да се променя по-бързо или по-бавно.
Производното функцията на графиката. Геометрична смисъла на производното
Сега нека видим как да се намери производната използване на графиките:

Нека да разгледаме нашия график функции: Равенство в гр абсциса x0 допирателната към графиката на функцията. Tangent и график на нашата функция в контакт в точка А. Трябва да се оцени колко стръмно отива графика на функцията. Удобен стойност за това - наклона на допирателната.
Определение. Производното на функцията на точка x0 е равен на наклона на допирателната към графиката на функцията в тази точка.
Ъгълът на наклона на допирателната е избран като ъгълът между допирателната и положителната посока на оста х.
Така че производната на нашата функция е равна на:
И така, производна на x0 е наклонът на допирателната е геометричен смисъл на производната.
Алгоритъмът за намиране на функцията производно
Алгоритъмът за намиране на производно функция у = F (х).
а) За да се определи стойността на х, за да се намери е (х).
б) Да се намери нарастване на аргумент х + Δx и функцията на стойността на нарастване на е (х + Δx).
в) Намери нарастване Δy = F функция (х + Δx) -f (х).
г) Създаване на връзка: Δy / Δx
г) Изчисли
- то е производно на нашата функция.
диференциация на функции
Ако функция у = F (х) е производно в точка х, то се нарича диференцируема в точката х. Процесът на диференциация нарича производно функция у = F (х).
Нека се върнем към въпроса за непрекъснатост на функцията. Ако функцията е диференцируема в даден момент, а след това на графиката на функцията в този момент, може да се направи функция тангенс не може да има прекъсване в този момент, а след това просто не може да се направи тангента.
И така, можем да пишем по-горе каза, като определението:
Определение. Ако функцията е диференцируема в точката х, то е непрекъснат в този момент.
Въпреки това, ако функцията е непрекъсната в точка, това не означава, че тя е диференцируема в тази точка. Например, у функция = | х | при х = 0 е непрекъсната, но не може да побере допирателна и следователно производно не съществува.
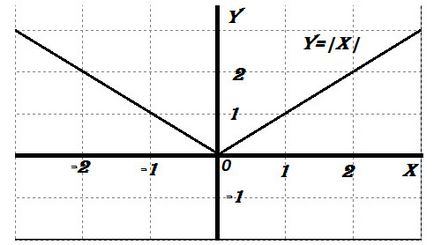
примери на производното
Виж производното на функцията: у = 3x
решение:
Ще използваме алгоритъм произлиза търсенето.
1) За фиксирана стойност на х, стойността на функция у = 3x
2) В точка х + Δx, у = F (х + Δx) = 3 (х + Δx) = 3x + Δx 3
3) Виж функцията увеличение: Δy = е (х + Δx) -f (х) = 3x + 3 Δx-3x = 3Δx
4) образуват връзка:
5) Да се намери границата:
Отговор: F '(х) = 3
Виж производното на функция у = 5х 2
решение:
Ще използваме алгоритъм произлиза търсенето.
1) За фиксирана стойност на х, стойността на функция у = 5х 2
2) В точката х + Δx, у = е (х + Δx) = 5 (х + Δx) ^ 2 = 5 (х 2 + 2xΔx + Δx 2)
3) Намерете нарастване на функцията:
Δy = е (х + Δx) -f (х) = 5x 2 + 10xΔx + 5Δx -5x 2 2 = 10xΔx + 5Δx 2
4) образуват връзка:
Виж производното на у = 2 х 2 + 1 -x
Ще използваме алгоритъм произлиза търсенето.
1) За фиксирана стойност на х, стойността на функцията
2) В точката х + Δx, у = е (х + Δx) = 2 (х + Δx) 2 - (х + Δx) + 1 = 2 (х 2 + 2xΔx + Δx 2) - (х + Δx) 1
Намираме функцията увеличение: Δy = F (х + Δx) -f (х) = = 2 х 2 + 4xΔx + 5Δx 2 - (х + Δx) + 1-2x 2 + х-1 = = 4xΔx + 5Δx 2 -Δx
3) образуване на връзката: