Репетиция графично изобразяване на квадратна функция
За да се направи графика на функция в правоъгълна координатна система, трябва две перпендикулярни линии XOY (където О е превантивна точка на х и у), които се наричат "координатни оси", и единица мярка.


На мястото има две координати в тази система.
М (х, у): M е името на точката, х е абсцисата, и тя се измерва от вол и у е ординатата и изправен в Oy.
Две координати представлява разстоянието от точката на двете оси.


Ако разгледаме функция F: А -> B (където А - домейн, B - площ функционални стойности), тогава точката на графиката на тази функция може да бъде представен във формата Р (х, е (х)).
пример
е: А -> В, е (х) = 3x - 1
Ако х = 2 => е (2) = 2 х 3 - 1 = 5 => Р (2, 5) в; Gf (където Gf е графика на тази функция).
квадратна функция
Стандартната форма: е (х) = ос 2 + BX + в
Ако> 0. след минималната стойност на е (х) е $ - \ Frac $. която се получава, когато $ х = - \ Фрак $. График е изпъкнал парабола. връх (точката, в която тя се променя посоката) е $ V (- \ Фрак; - \ Фрак) $.


Ако <0. то минимальное значение f(x) будет $-\frac$. которое получается, если $x=-\frac$. Графиком будет вогнутая парабола. вершина которой это$V(-\frac;-\frac)$.
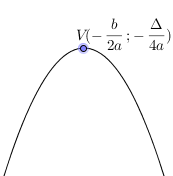

Парабола симетричен по отношение на права линия, която го пресича $ х = - \ Фрак $ и се нарича "оста на симетрия".
Ето защо, когато се възлага znayacheniya х. на vibiraem ги симетрични по отношение на $ - \ Фрак $.
Когато изобразени, точките на пресичане с координатните оси са много важни.
|. Точка, разположена върху оста Ox е под формата Р (х, 0). защото разстоянието от него, на ОХ е равен на 0. Ако точката се намира на Ox и функцията графика, той също има форма Р (х, е (х)) → е (х) = 0.
По този начин, за да намерите координатите на точката на пресичане с Ox на ос. трябва да реши уравнение е (х) = 0. Ние получаваме уравнението 2 + BX + с = 0.
Решението зависи от знака на уравнението δ = б 2 - 4ав.
Immem следните опции:
1) δ <0 ,
тогава не съществуват решения на уравнението R (определени на реални числа) и графиката пресича Ox. Форма на графиката е:




2) δ = 0,
след две решения на уравнението $ x_1 = x_2 = - \ Фрак $
Що се отнася до графика ос Ox в връх на параболата. Форма на графиката е:




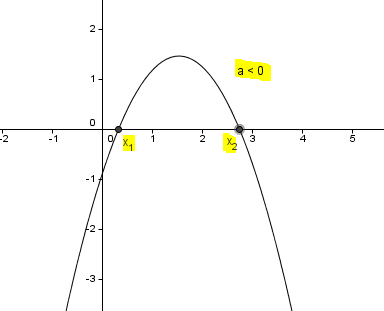
3) δ> 0,
след уравнението две различни решения.
Графиката на Ox ос ще се пресичат в точки М (х 1 и Ox се генерира вид .:



||. Точка на оста Oy е във формата на R (0, у). защото разстоянието от Oy е 0. Ако точката се намира на Oy и функцията графика, той също има форма R (х, е (х)) → х = 0 → R (0, F (0)).
В случай на квадратна функция,
F (0) = а х 0 + б х 2 0 + в → R (0, в).
Необходими стъпки графика на квадратна функция
е: R → R
е (х) = брадва 2 + BX + в
1. маса на променливи, където преспи са някои важни стойност на х.
2. Изчисляване на координатите на връх $ V на (- \ Фрак; - \ Фрак) $.
3. Също така, напиши 0 в таблицата и нулеви стойности симетричен $ - \ Фрак $.
4. Ние дефинираме точката на пресичане с оста Ox чрез решаване на уравнение е (х) = 0 и запис x1 и x2 корени в таблицата.
δ> 0 →
δ <0 → точек пересечения нет. В этом случае мы выберем два удобных значения, которые симметричны $-\frac$
δ = 0 → график отнася Ox точно в върха на параболата. Ние отново да избере две удобни стойности на симетричен $ - \ Фрак $. За да можем да изберем други двойки стойности за х-добро определяне на формата на графиката. но те трябва да са симетрични $ - \ Фрак $.
5. Ние събрахме тези ценности в координатната система и изграждане на графика, като свържете тези точки.
ПРИМЕР 1
е: R → R
е (х) = х 2 - 2х - 3
а = 1, б = -2, с = -3
δ = б 2-4 х а х с = (-2) с 2 - 4 х 1 х (-3) = 16
$ - \ Frac = \ Frac = 1 $ → V (1; 4)
2. е (0) = -3
Symmetrical 0, стойност 1 е 2.
е (2) = -3
Графиката ще изглежда така:

Пример 2
е: R → R
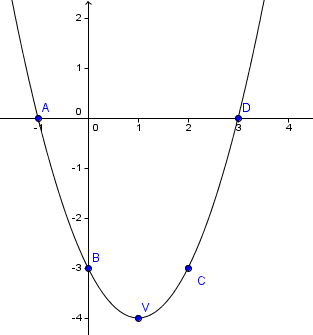
е (х) = -x 2 - 2х + 8
а = 1, б = -2, с = 8
δ = б 2-4 х а х с = (-2) с 2 - 4 х (-1) х 8 = 36
$ - \ Frac = \ Frac = -1 $ → V (1; 9)
2. е (0) = 8
е (-2) = 8 (симетрична по отношение на стойността 0 е равна -1 -2)
А (-4 0)
B (-2; 8)
V (1; 9)
C (0; 8)
D (2, 0)


ПРИМЕР 3
е: R → R
е (х) = х 2 - 4x + 4
а = 1, б = -4, с = 4
δ = б 2-4 х а х с = (-4) с 2 - 4 х 4 х 1 = 0
$ - \ Frac = \ Frac = 2 $ → V (2, 0)
2. е (0) = 4
F (4) = 4 (симетрична по отношение на стойността 0 е 4 2)
А (-2; 9)
B (0, 4)
V (2, 0)
С (4, 4)
D (5, 9)


ПРИМЕР 4
е: R → R
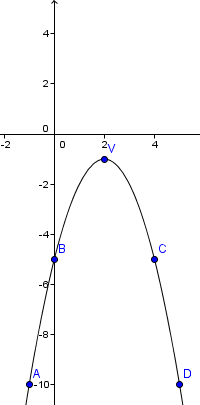
е (х) = -x 2 + 4x - 5
а = 1, б = 4, с = -5
δ = б 2-4 х а х с = 2 4-4 х (-1) х (-5) = 16-20 = -4
$ - \ Frac = \ Frac = 2 $ → V (2, 1)
2. е (0) = -5
F (4) = -5 (симетрична по отношение на стойността 0 е 4 2)
3. е (х) = 0 → -x 2 + 4x - 5 = 0, δ <0
Това уравнение все още няма решения. Избрахме симетрична стойност около 2
А (1; -10)
B (0, 5)
V (2, 1)
С (4; 5)
D (5, -10)

Ако домен не е R (набор от реални числа), и някои интервал, след това изтриване на част от графиката, която съответства на тези стойности на х, които не са в този диапазон. Необходимо е да се запишете крайни точки интервалните в таблицата.
Пример 5
е: [0; + ∞) → R
е (х) = х 2 - 2х - 3
а = 1, б = -2, с = -3
δ = б 2-4 х а х с = (-2) с 2 - 4 х 1 х (-3) = 16
$ - \ Frac = 1 $ → V (1; 4)
2. е (0) = -3
е (2) = 0, стойността -3 симетрична по отношение на една е равно на 2)
3. е (х) = 0 → х 2 - 2х - 3 = 0, δ = 16
X1 = -1 ∉ [0; ∞)
х2 = 3
А (0, -3)
V (1; 4)
B (2, 3)
C (3, 0)

