Решаването на проблемите по темата - пирамида
Вашият браузър не поддържа вложени фреймове!
Урок Цели:- образователна:
- опознаването на евристика;
- извлече формули основните ъгли преход в правилните пирамиди;
- научите как да използвате евристика, за да докаже, взаимоотношения между ъгли в правилната пирамидални и решаване на проблемите.
- Развитие:
- развие познавателни интереси чрез развитие на уменията на младите изследователи;
- развие форма на паметта, абстрактно и логическо мислене;
- да развият компютърни умения на студентите.
- образователна:
- ваксиниране на комуникативни умения, с дидактически умения материални (брошура, електронен ресурс);
- генерира точно изпълнение на действията при изпълнение на практическа работа и групова работа.
- компютър
- проектор,
- екран,
- интерактивна бяла дъска, SMART Board,
- милостиня
I. Организационни въпроси
- Моля, отворете една тетрадка и си запишете номера и темата на урока: Решаване на проблеми на "Пирамида". Днес в клас ние сме за решаване на проблемите се научите как да се приложи по поръчка рецепция, наречен евристика. Ние извлече формулите за прехода на основни ъгли на правилните пирамиди и да се научат да ги прилагат при решаване на проблеми.
- За да направите това, ние трябва да се повтаря някои от въпросите от хода на геометрията.
Орална работа (фронтална проучване).
Дан правоъгълен триъгълник ABC.

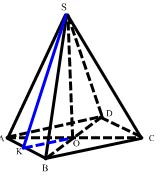
- Какво полихедронов се нарича пирамидална схема?
- Какви са на върха на пирамидата? Фондация?
- Какво пирамида, наречена нали?
- Къде очакваната височина на редовен пирамида?
- Име на ъгъла между страничния ръб и на основата на пирамидата; Между страничната стена и основа; ъгълът между страничните стени на пирамидата?
Помислете за решаването на проблема от учебник. Внимание на дъската.
№ 255. редовен триъгълна пирамида база край е 8 см и плосък връх на ъгъла на равно да получите височината на пирамидата.
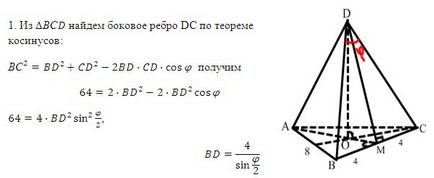
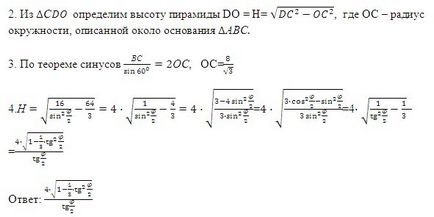
III. Формиране на нови знания
За решаване на проблема, ние трябваше да се справят с триъгълници, които не лежат в една равнина, а освен това, всеки един от тях е известно, че не повече от два елемента. Какво мислите, има ли някакви математика по един по-прост начин за решаване на проблема? Бих казал, че има! Всъщност, този процес съществува. И това си има име мнемоничен решаване на геометрични задачи. Тя е от него, че аз ви представим днес. Така че ...
Мнемоника (от гръцки - паметта) - различен вид на техники, които насърчават изкуствено запаметяване. С други думи - това е изкуството на запаметяване. Още древните и диваците са известни редица техники, които дават точки за подкрепа памет. Можете също така, че някои мнемонични техники, като например съхранение на цветовете на дъгата, определението на ъглополовящата и др.
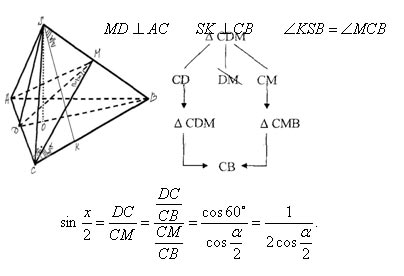
Така че, евристика <Приложение 3> зависимостта между ъглите в правилната пирамида:
1. Ние пишем тук триъгълник, в който ъгълът е неизвестен.
2. От трите букви S, А, О съставят различни двойки. Получихме три сегмента.
3. Зачеркнете този, който не се среща често, за да триъгълници, които имат известни ъгли.
4. Нека добавим в писмото, за да получите името на триъгълник, състоящ се от един от тези ъгли:
5. Намерете сегмента, състоящ се от буквите в общ.
6. За да се постигне изискваното зависимостта разделят числителя и знаменателя на намерен сегмент.
- Сега, с този евристика, ще получите някаква връзка между ъгли в правилната пирамида.
1. Връзката между равнинен ъгъл при върха на пирамидата и правилен ъгъл на база ръб (четириъгълна пирамида) на
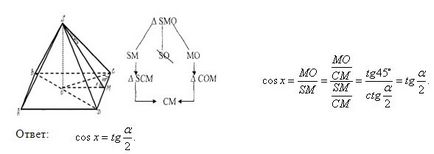
2. Връзката между плосък ъгъл в горния десен ъгъл на пирамидата и страничен ръб
IV. Формиране на основните умения
Уважаеми 10-tiklassniki. Сега, в практическата работа, вие ще изследва връзката между ъглите на пирамидата в отдясно, оставяйки всяка група ще се получи преход формула. Всяка група има своя задача. Вие сте на масата с листове със задачи <Приложение 2> и помага на паметта <Приложение 3>. което ще ви позволи да намерите бързо необходимите зависимости.
Учениците работят в групи. В края на представителна група с формула прави полученият прехода в таблицата на плъзгача.
Всяка група се появи на маса сигнал червен картон.<Приложение 4>С нея можете да проверите коректността на тяхното мислене.

В резултат на практическата работа, ние имаме една връзка между маса ъгли в правилната пирамида. В следващия етап от нашата урок, ние ще се прилага формулата за решаване на проблемите, и едновременно с това се прецени колко тези формули улесняват живота ни.
Да се върнем към проблема, който е решен в началото на урока. (В плъзгача с разтвор и завеса с използване на преходни формули)
Друг начин да се реши

Очевидно е, че с помощта на преход формули трудности при решаването на проблемите са лесно преодолени. Имате на масата е таблица на формулите за преход <Приложение 5> не само да триъгълна и четириъгълна пирамида, но също така и за шестоъгълна и п-въглища. Тези формули могат и трябва да се използват при решаването на проблемите.
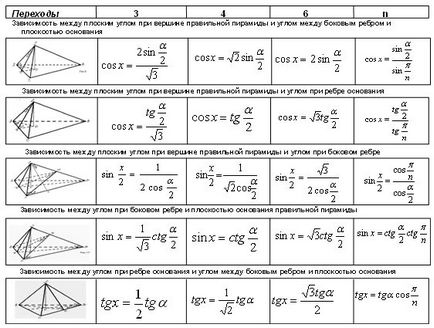
Помислете за прилагането на формулите за други задачи в учебника
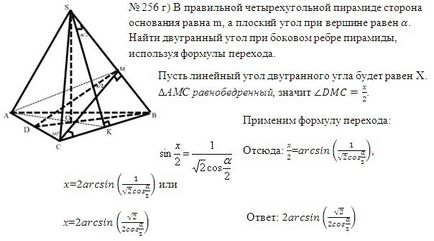
Въпреки това, една красива решение?
- Днес ще се срещна с мнемонични трикове, за да се намери връзката между ъглите в редовен пирамида, и използваха евристика, някои от тези зависимости, и да ги прилагат за решаване на проблемите.
Решаване на сложни проблеми stereometric често имат проблеми. Те могат да възникнат по-специално, тъй като данните, предоставени в линейни елементи не принадлежат към една и съща равнина, и поради това, че няма такова право триъгълник, с които да се започне с решение. Въпреки това, с помощта на евристика и да се премести формули трудности лесно се преодоляват.
За своята работа по оценката, следващия урок, учениците ...
VII. домашна работа
За домашна работа, предлагам ви да разрешите проблема 254 (б, D, E) по два начина: традиционни и с помощта на евристика (преход формули).
- Благодаря ви за урока