Решение на системата от линейни уравнения

Системата на линейни уравнения

уравнение система обикновено е написано в колона една над друга и са комбинирани скоба

Системата от уравнения на формата, където А, В, С, - броя и X, Y - променливи, се нарича система линейни уравнения.

В решаването на системата уравнения използвайки свойствата, просто за решаване на уравнения.

Разтворът на система линейни уравнения метод смяна

1) изрази променлива в един от уравнения. Например, можем да експресират у в първото уравнение, ние получаваме системата:

2) заместител в второто уравнение на мястото на 3-ил експресия 7:

3) решаване на получения второто уравнение:

4) Полученият разтвор е заместен в първото уравнение на системата:

Системата от уравнения има уникален разтвор: чифт числа х = 1, у = -4. Отговор: (1; 4). Писано е в скоби, първият х позиция стойност. втората - у.

Разтворът на система за линейни уравнения метод на прибавяне

Ние решаването на системата от уравнения на предходния пример по метода на прибавяне.

1) Конвертиране на системата, така че коефициентите на една от променливите стават обратното. Умножете първото уравнение на системата за "3".

2) Fold termwise уравнение система. Вторият уравнението на системата (такива) пренаписване непроменена.

3) Полученият разтвор е заместен в първото уравнение на системата:

Решение на системата от линейни уравнения графично

Графични решаване едновременни уравнения с две променливи е намалена до координатните точки в общи извличане уравнения графики.

Графиката на линейна функция е права линия. Две линии в равнината може да се пресичат в една точка, за да бъде успоредна или съвпадат. Следователно, системата от уравнения може: а) да има уникален разтвор; б) не са разтвори; в) имат безкраен брой решения.

2) система от уравнения е точката (ако уравнения са линейни) пресечните графики.

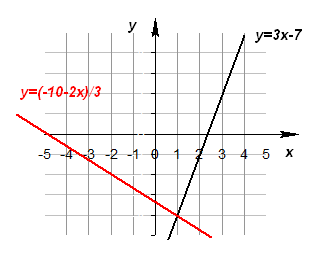
Графично решение на системата

Методът за въвеждане на нови променливи

Заместващите променливи могат да доведат до решаването на проста система уравнение от оригинала.

Помислете за решаването на системата

Въвеждаме замяна, а след това

Обръщаме се към оригиналните променливи

специални случаи

Без решаването на система от линейни уравнения, ние можем да се определи броя на своите решения върху коефициентите на съответните променливи.

Като се има предвид система

1) Ако системата има уникално решение.

2) Ако системата все още няма решения. В този случай, преките, е графиката на системата от уравнения са успоредни и не съвпадат.

3) Ако в системата има безкраен брой решения. В този случай, линиите съвпадат един с друг.

Методът последователно елиминиране на неизвестни, в резултат на система за линейни уравнения за ешелон форма.