серия Номер

1. Основни понятия

Нека u1, u2. U3. ..., ООН. ...  безкраен последователност от числа. изразяване

nazyvaetsyabeskonechnym числова поредица. брой u1, u2. U3. ..., ООН  членове на серията; Тя се нарича общ термин от поредицата. Няколко често написани на съкращение (сгънат) форма:

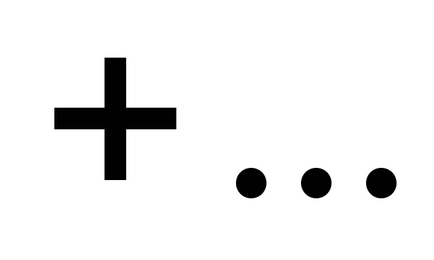
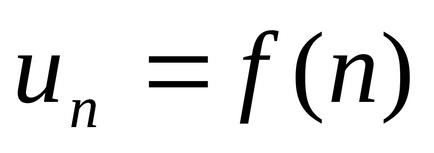
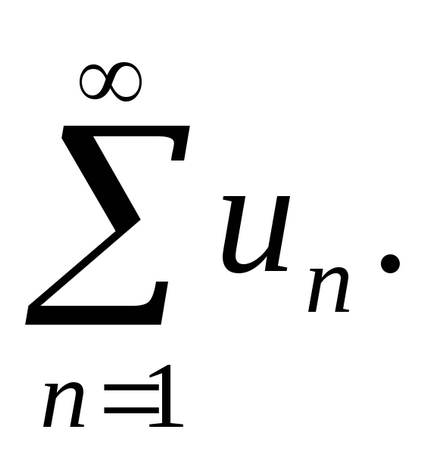
Сумата от първите N членовете на поредица от числа означен

и nazyvayutn та частична сума от серията:

.

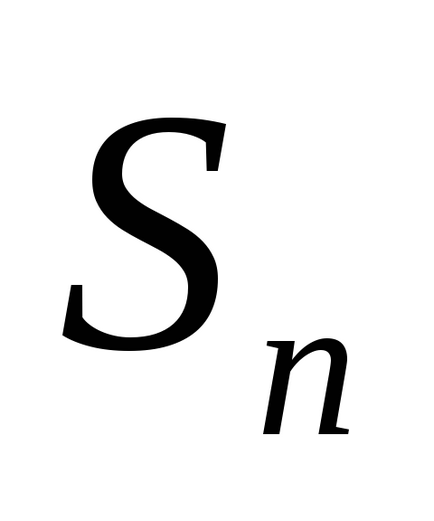
Series се нарича сходни. ако п-тата частична сумата

неограничения vozrastaniin подходи границите на допустимите, т.е. ако номерnazyvayutsummoy серия.

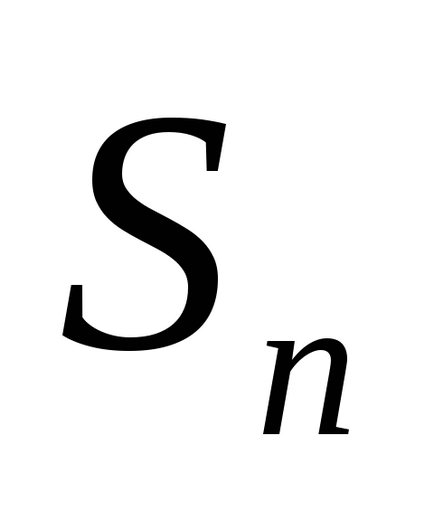
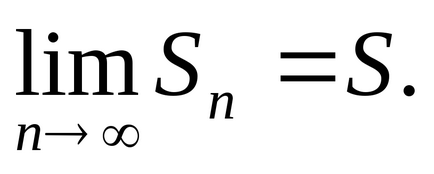
Ако п-ти частично сумата от серията на

Това не са склонни да се границите на допустимите, броят на nazyvayutraskhodyaschimsya.

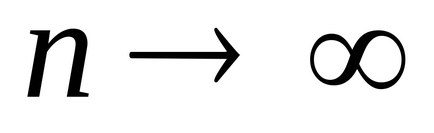
Пример 1. Намерете сумата от серията.

Решение. имаме

. Тъй като:

,

.

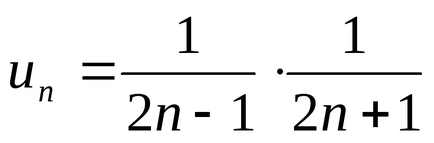
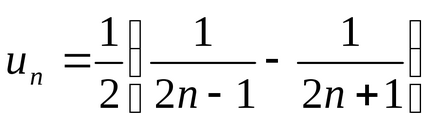
Оттогава поредицата клони и неговата сума е

.

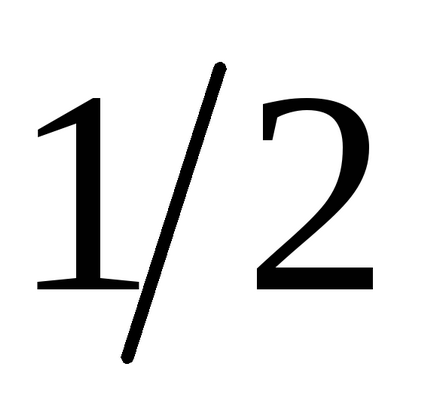
2. Основните теореми на числова поредица

Теорема 1. Ако серията

сближаването на сериятаПолучената от изхвърляне на множество първичленове (последният номер, наречени-m част на оригиналната поредица). От друга страна, за конвергенция-тата остатък от поредицата предполага сближаване на поредицата.

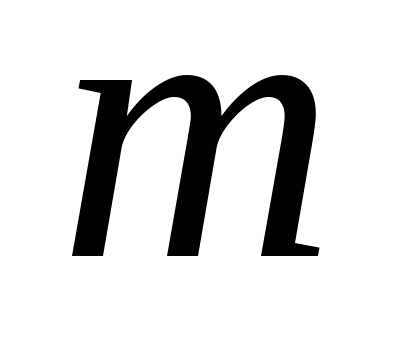
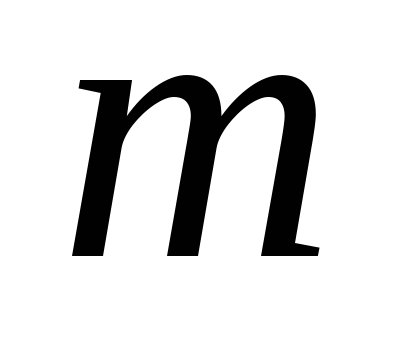
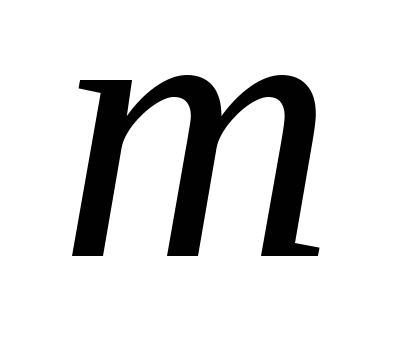
Теорема 2. Ако поредицата и това е сумата от броя на

, След това се доближава количество ryadprichem равен на последния ред.

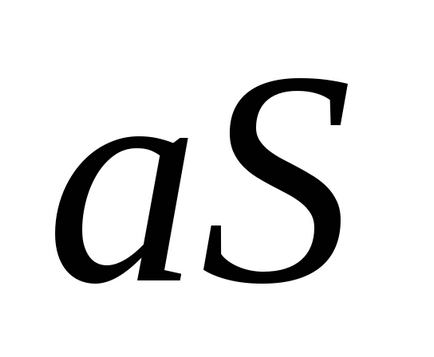
Теорема 3. Ако сте съгласни с редове съответно summyS и Q, клони серията и сумата е равна на последния ред

.

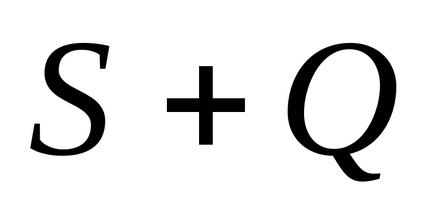
Теорема 4 (времето, необходимо за засилване на сближаването на серията). Ако серията клони,

, т.е. прилимит от общия брой на членовете на конвергентни е нула.

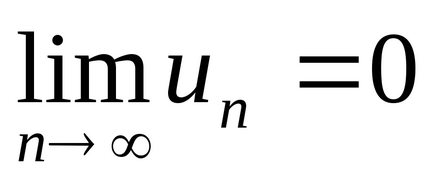
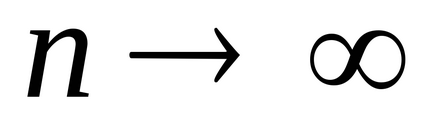
Следствие 1. Ако

, След това серията се отклонява.

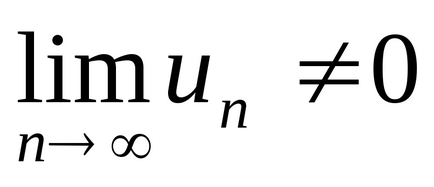
Следствие 2. Ако

, след това се определя сближаването или разминаване на поредицата с помощта на критерия необходима сближаване не трябва да бъде. Редица може едновременно конвергентна и дивергентна.

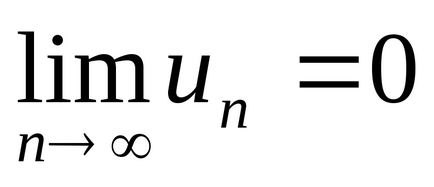
Пример 2. Разглеждане на сближаването на серия:

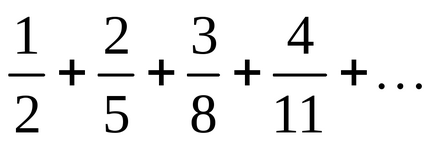
Решение. Намерете общ термин от поредицата. Тъй като:

,

т.е.

, След това се различава серията (не притежава необходимото условие за сближаване).

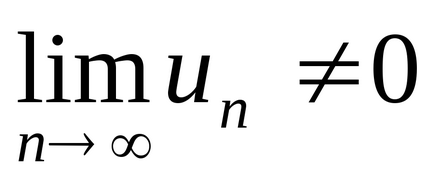
3. Признаци на сближаване на серия с положителна

3.1. директен сравнителен тест

Пряко сравнение тест на базата на сравнение на предварително определен брой конвергенция с редица конвергенция или разминаване на която е известна. За сравнение, като се използва по-долу изброените серия.

ред

съставен от членове на всяко намаляване на геометрична прогресия е конвергентна и има сума

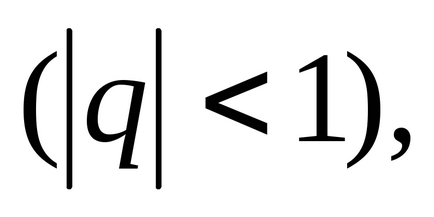
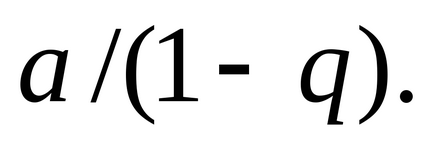
ред

съставен от членове, нараства експоненциално, то е за отклоняване.

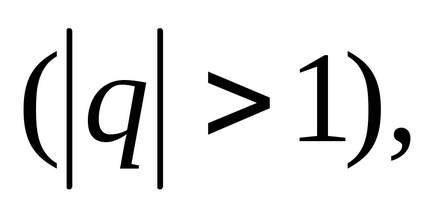
ред

Тя е за отклоняване.

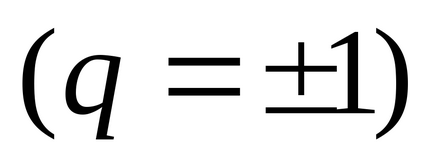
Series се нарича Дирихле серия. Pri> 1 серия Дирихле клони в <1- расходится.

Когато  = 1 серия

Тя се нарича хармонична. Хармоничните серии се отклонява.

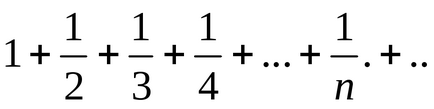
Теорема. Първият знак за сравнение. две серии с положителна Да предположим, че:

където всеки член на серия (1) не надвишава съответния брой елементи (2), т.е.

(N = 1, 2, 3, ...). Тогава, ако поредицата (2), сближаването на серия (1); Ако обхвата на дебит (1), разсейването и серия (2).

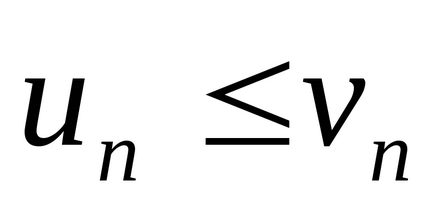
Забележка. Тази функция остава в сила, ако neravenstvo

Тя не се извършва за всички, но само като се започне от определен бройп = Н. т.е. всички nN.

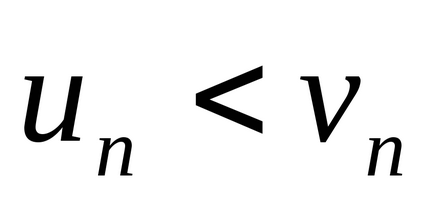
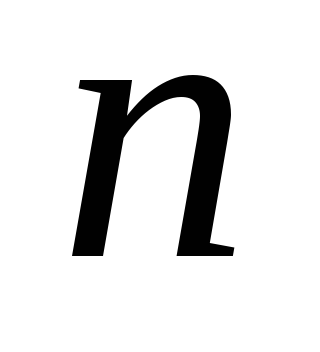
Пример 3: Да се ​​проучи сближаването на

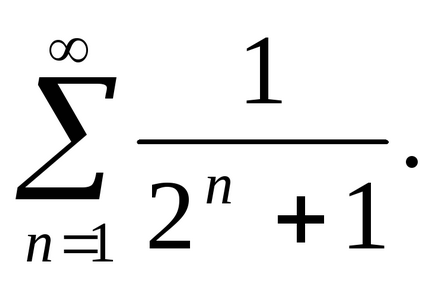
Решение. Членовете на серията по-малко от съответните условия на серията

съставен от членове на безкрайната геометрична прогресия. От тази серия клони, а след това се слива и по един номер.

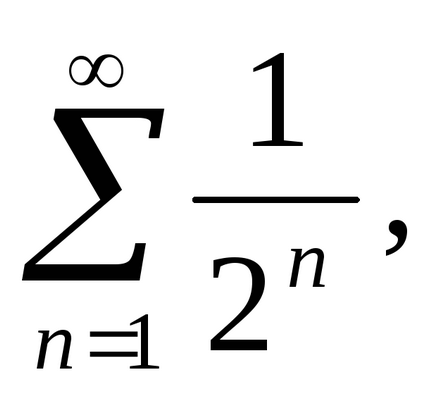
Теорема. втората Сравнението на функция (сравнение тест ограничаване форма). Ако има краен и не нулев лимит

, а след това и двете серииисъбират или различават едновременно.

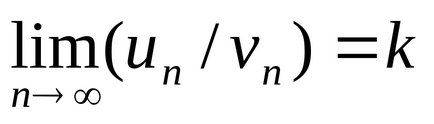
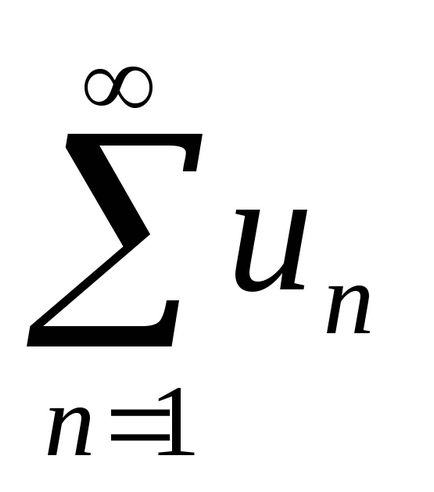
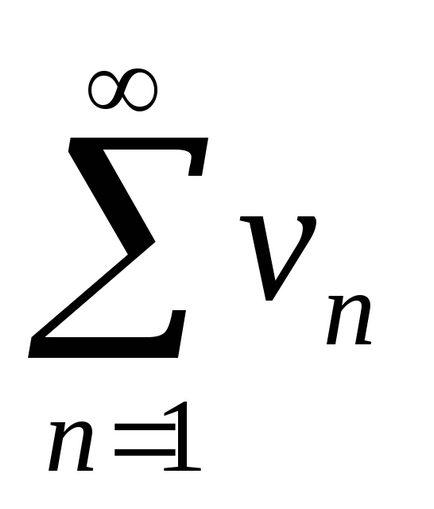
Пример 4. За да се изследва за конвергенция на

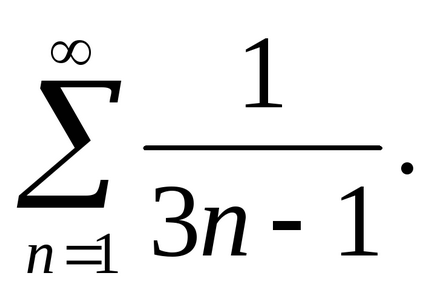
Решение. Сравними с броя на хармоничните серии

Ние намираме на границата на отношението на общите условия на серията:

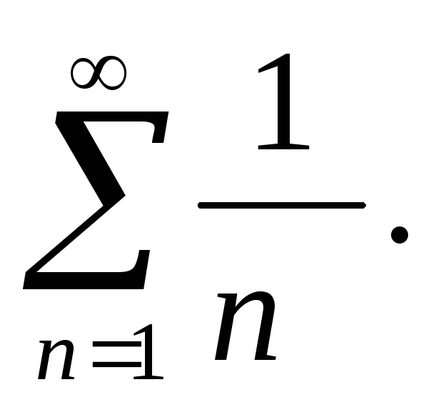
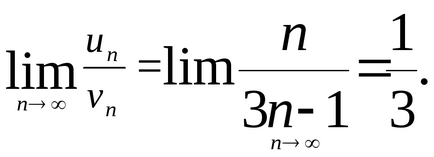
От хармоничните серии се отклонява, а след това се отклонява и по един номер.