Случайни променливи

Дискретни и непрекъснати случайни величини

Един от основните понятия на теорията на вероятностите е концепцията за случайна променлива. Произволна стойност е стойност, която е резултат от теста на множество възможни стойности на тяхната отнема само един, освен това не е известно кой.

Случайни променливи са дискретни и непрекъснати. Дискретни случайна стойност (DSV) е случайна променлива, която може да се определен брой изолирани помежду си стойности, т.е. Ако могат да се отчитат възможните стойности на тази величина. Непрекъснато случайна стойност (НСВ) е случайна променлива, всички възможни стойности, които напълно запълни определен брой линия интервал.

Случайни стойности са отбелязани с главни латински букви X, Y, Z, и т.н. Възможните стойности на случайни променливи са обозначени със съответните малки букви.

Запис означава "вероятността случайна променлива заема стойност от 5 е равен на 0.28."

Пример 1. След хвърляне на зара. В този случай, може да падне число от 1 до 6, което показва броя на точките. Означаваме случайни променливи X =. Това случайна стойност като резултат от изпитването може да се само един от шестте стойности: 1, 2, 3, 4, 5 или 6. Следователно случайна променлива X е DCB.

Пример 2. Когато хвърляне на камък, той лети известно разстояние. Означаваме случайни променливи X =. Тази случайна променлива може да има такива, но само един, стойността на определен период от време. Следователно, случайна променлива X е PDR.

Акт дискретна случайна променлива разпределение

Дискретна случайна променлива се характеризира със стойности, че да може да и вероятностите с които се вземат тези стойности. Съответствието между възможните стойности на дискретна случайна променлива и съответните вероятности се нарича закон на дискретна случайна променлива разпределение.

Ако всички възможни стойности

случайна променлива и вероятността появата на тези стойности, се счита, че DSVH разпределителната право са познати и може да бъде написана под формата на таблица:

закон DSV разпределение може да бъде представен графично, ако правоъгълна координатна система, за да представя гледната

,, ...,





и свързването им по сегменти на прави линии. Полученото число се нарича разпределение многоъгълник.

Пример 3. Зърното да се почистват, съдържа 10% от плевелите. 4 произволно избрани зърна. Означаваме случайни променливи X =. Изграждане на закона разпределение DSV X и разпространение многоъгълник.

Решение. Например състоянието. След това:

;

;

;

;

.

Пишем закона на разпределение на DSV X под формата на маса и изграждане на разпределение на полигон:

Очакване DSV X е сумата от всяка стойност на това количество на съответния вероятността :.

Очакването на случайна променлива е приблизително равен на средната аритметична стойност на неговите ценности. Затова в практически проблеми често е под очакванията на средната стойност на тази случайна променлива.

Primer8. Стрелецът Emboss 4, 8, 9, и 10 точки на вероятностите за 0.1, 0.45, 0.3 и 0.15. Намери очаквания брой точки в един изстрел.

Решение. Означаваме случайни променливи X =. След това. По този начин, се очаква средният брой на разпръснати в един изстрел точки е равна на 8,2, а в 10 изстрела - 82.

Основните свойства на очакването, са:

.

.

.

, където X и Y - са независими случайни променливи.

разлика

nazyvaetsyaotkloneniem случайна променлива X от неговата очакване. Тази разлика е случаен и нейното математическо очакване е равно на нула, т.е. ,

Дисперсията на дискретна случайна променлива

За характеризиране на случайна променлива с изключение на математически очакването и се използва дисперсията. което прави възможно да се оцени стойностите дисперсия (вариант) на произволна променлива около своята очакване. При сравняване на два еднакви случайни величини с математически очаквания са равни "най-доброто" стойност е този, който има по-малък обхват, т.е. малък вариацията.

Отклонението на случайната променлива X е математическо очакване на квадрата на отклонението на случайна променлива от неговото математическо очакване :.

В практически проблеми за изчисляване разрез с помощта на еквивалентна формула.

Основните свойства на дисперсията са:

.

.

, където X и Y - са независими случайни променливи.

Дисперсия характеризира дисперсията на случайната променлива около нейната средна и както се вижда от формула, измерена в квадратни единици в сравнение с дяловете на случайна променлива. Ето защо, стандартното отклонение въведени единици за хармонизация разпространяват измерване случайна променлива със стойността на мерни единици

.

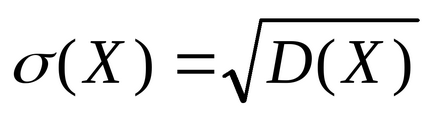
Primer9. Намерете дисперсията и стандартното отклонение на DSV H. предварително определен закон разпределение: