Как да се намери радиуса на кръга, описан около триъгълник

Кръгът може да бъде вписан четириъгълник ако + с = б + д, където А, В, С, D - четириъгълник страна в ред. Около обиколката на четириъгълника може да се опише, ако обратното на неговите ъгли добавите до 180 градуса;

За триъгълник винаги съществуват такива кръгове.

Търсене площ на триъгълника - един от най-често срещаните задачи на училище планиметрия. Познаването на трите страни на триъгълник е достатъчно, за да се определи площта на всеки триъгълник. В конкретни случаи, равнобедрен и равностранен триъгълник достатъчно да се знае дължината на две и едната страна съответно.

• дължина на страните на триъгълници, херонова формула, теоремата на косинус

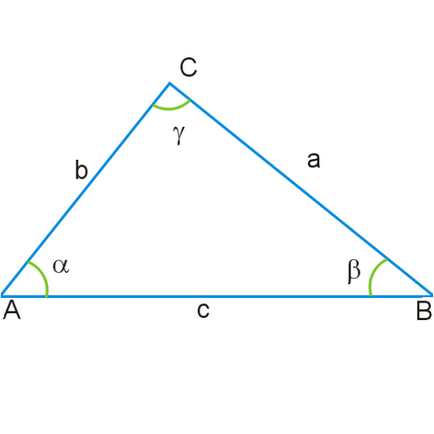
Като се има предвид един триъгълник ABC със страници AB = с, AC = б, BC = а. Площта на такъв триъгълник може да се намери от формулата на чапла.

Периметърът на триъгълника P - е сумата от дължините на трите страни: P = A + B + C. Ще означаваме го semiperimeter за стр. Това ще бъде равно на р = (A + B + C) / 2.

формула чапла за областта на триъгълника е както следва: S = SQRT (р (р-а) (р-Ь) (р-с)). Ако боя semiperimeter р, получаваме: S = SQRT (((а + б + в) / 2) ((б + ва) / 2) ((а + в б) / 2) ((а + бв) / 2) ) = (SQRT ((A + B + C) (а + бв) (а + в б) (б + кз))) / 4.

Възможно е да се получи формула за областта на триъгълник и други съображения, например, с помощта на теоремата на уют.

Според теоремата на уют AC ^ 2 = (АВ ^ 2) + (пр ^ 2) -2 * AB * пр * COS (ABC). Използването на тази система за означаване, експресирането може също да бъде в писмена форма: B ^ 2 = (а ^ 2) + (С ^ 2) 2а * C * COS (ABC). Следователно, COS (ABC) = ((а ^ 2) + (С ^ 2) - (Ь ^ 2)) / (2 * а * в)

Площта на триъгълника също е съгласно формула S = А * С * грях (ABC) / 2 чрез двете страни и между тях ъгъл. ъгъл синусите ABC може да се изрази чрез косинус използване на основни тригонометрични идентичности :. Sin (ABC) = SQRT (1 - ((COS (ABC)) ^ 2) Заместването задължително формула за областта и писане може да се стигне до формула за областта ABC.

Трите точки еднозначно определят триъгълник в Декартова координатна система - е неговата най-добре. Знаейки им положение спрямо всяка от координатните оси могат да бъдат изчислени някои параметри на равнина фигура обградени от и включително периметъра на своята област. Това може да стане по няколко начина.

Използвайте формула на Херон за изчисляване на площта на триъгълник. В него са участвали размера на трите страни на фигурата, така че изчисленията, тъй като тяхното определяне. Дължината на всяка страна трябва да бъде равен на корен квадратен от сумата от квадратите на дължините на прогнози си върху осите. Ако означават координатите на точките А (X,, Y₁, Z₁), В (X₂, Y₂, Z₂) и С (X₃, Y₃, Z₃), дължините на техните страни може да се изрази както следва: AB = √ ((X,-X₂) ² + ( Y₁-Y₂) ² + (Z₁-Z₂) ²), BC = √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²), AC = √ ((X,-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).

За опростяване на изчисленията, влиза спомагателната променлива - semiperimeter (Р). Както подсказва името, е половината от сумата на дължините на всички страни: P = Уг * (AB + BC + AC) = Уг * (√ ((X,-X₂) ² + (Y₁-Y₂) ² + (Z₁-Z₂) ²) + √ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²) + √ ((X,-X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²).

Изчислява областта (S) с формула чапла - премахване semiperimeter корен на продукта от разликата между него и дължината на всяка страна. Като цяло си форма може да бъде написано, както следва: S = √ (P * (P-AB) * (Р-BC) * (Р-AC)) = √ (P * (P-√ ((X,-X₂) ² + ( Y₁-Y₂) ² + (Z₁-Z₂) ²)) * (P-√ ((X₂-X₃) ² + (Y₂-Y₃) ² + (Z₂-Z₃) ²)) * (P-√ ((X, -X₃) ² + (Y₁-Y₃) ² + (Z₁-Z₃) ²)).

полетата на формата отделно влизат всяка координата на всеки един от върховете на триъгълника - те са посочени тук като брадва, Ay, AZ и т.н. Ако триъгълник е дадена двуизмерни координати в областта на Z - Az, BZ и CZ - пише нула. В "изчисляване Precision" на задаване на желания брой знака след десетичната запетая, като кликнете върху иконата на мишката плюс или минус. Поставени под формата на оранжев "Изчисли", за да натиснете не е необходимо, изчисления ще бъдат направени без него. Отговорът ще намерите в непосредствена близост до "триъгълник зона" - тя се намира точно под оранжевия бутон.

• намерите на триъгълника с върхове

Понякога около изпъкнал многоъгълник може да начертаете кръг, така че върховете на всички ъгли, лежащи на него. необходимо е да се обадите такъв кръг по отношение на многоъгълника е описано. Центърът му не трябва да бъде вписан в периметъра на фигурата, но използването на свойствата на описаните окръжности. намерите този момент обикновено не е много трудно.

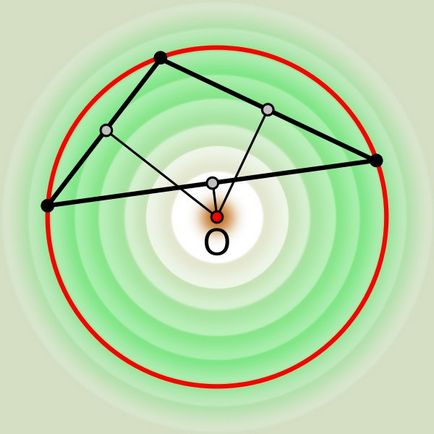
• Владетел, молив, транспортир или набор квадрат, компаси.

Ако многоъгълник, за който искате да се опише окръжност, изготвен на хартия, за да се намери в центъра на кръга и достатъчно на линия, молив и транспортир или полигон. Измерете дължината на всяка от фигурите на страните, определи средно и поставим на мястото на съставянето спомагателни точка. С многоъгълник или вътре многоъгълник транспортир пързалка, перпендикулярна на тази страна на сегмента до пресечната точка с противоположната страна.

Направете същата операция с всяка друга страна многоъгълник. Пресечната точка на два сегмента конструирани ще бъде желаната точка. Това следва от основните свойства на описаните окръжности - центъра на изпъкнал многоъгълник с произволен брой страни винаги се намира в midperpendiculars пресечните проведени с тези страни.

За определянето на правилен многоъгълник вписан кръг, а центърът може да бъде много по-лесно. Например, ако е квадратна, тогава изготвят два диагонално - и тяхното пресичане е центъра на вписан кръг ва. Във всеки правилен многоъгълник с четен брой страни достатъчни за свързване на две двойки помощни сегменти, разположени един срещу друг ъгли - центъра на окръжност кръг трябва да съвпада с момента на тяхното пресичане. В правоъгълен триъгълник, за да се реши проблема, просто обозначават средата на дългата страна на фигурата - хипотенузата.

Ако състоянието не се знае дали е възможно по принцип да се направи окръжности, за даден полигон, след определяне на предназначението централната точка и всяко едно от следните методи можете да разберете. Сложете на компас разстояние между намери място и някой от върховете в поставените разделители предполагаеми tsentrokruzhnosti и направи кръг - всеки връх трябва да лежи върху този кръг. Ако не е, тогава, не една от основните характеристики и опишете кръг около този полигон не могат.

Понякога в живота трябва да се справят със ситуации, които изискват познания по геометрия. Тази информация се използва рядко в ежедневието, така че да забравим. Един от най-популярните въпроси, е да се намери областта на триъгълник с помощта на дължините на двете страни.

Площта на триъгълника, който се изчислява в зависимост от дължината на двете му страни, също изисква измерване на ъгъла между тях. За да направите това, използвайте транспортир или други специални инструменти. Например, наклон - много удобен за измерване на ъгъл на стаята.

След като сте намерили размера на триъгълника двете страни и ъгълът между тях, отидете на изчисленията. Намирането на областта следва следната формула: SΔ ABC = 1/2 аб ъгъл грях. В същото време, ако имате под прав ъгъл в триъгълника между двете страни, известни, формулата може да бъде намалена: SΔ ABC = 1/2 AB.

За изчисляване на синуса на ъгъла, можете да използвате тригонометрични таблица Bradis, което дава стойности за най-често срещаните размери на ъгли. Друг добър начин за изчисляване на синуса на ъгъла е калкулатора. Във всяка от операционната система Windows е сред стандартните програми. Отвори я и се превключва на "Машиностроене", който е в раздела "Изглед". След това въведете размера на ъгъла, синуса на който искате да се изчисли. След това изберете единиците за изчислява отговор. Тя може да бъде градуса, радиани или развълнуван. Можете да направите това с помощта на бутоните под полето за въвеждане. Натиснете «грях» и да получите резултат.

Разбира се, синуса на ъгъла вече могат да бъдат изчислени с помощта на различни разширени онлайн калкулатори с удобен интерфейс и повече функции. Намерете подобна програма в интернет, не е трудно, защото те предлагат много. Просто въведете в търсачката "калкулатор тригонометричните функции" на.

Сега, умножаване двете страни на триъгълник на дължина и синуса на ъгъла между тях, разделете на две и всичко готов да отговори. площ на триъгълник е намерен.