Най-голямата стойност на експресията
За да намерите най-голяма стойност на тригонометрични изрази, в много случаи е достатъчно да се знае стойността площ от синус, косинус, тангенс, котангенс и свойства на неравенството.
Намерете максималната стойност на израза:
Диапазонът на допустимите стойности на този израз - целия номер ред:
ОБЛАСТ косинус стойности - интервала [-1; 1]. За да се оцени стойността е по-удобно да се използва двойно неравенство:
Умножете мандат със срок на неравенството 7. Когато се умножи по броя на положителните признаци на неравенство не се променят:
След това добавете план със срок 5:
По този начин, най-високата експресия стойност е равен на 12 (най-малките - -2, площ стойности - [-2: 12]).
Когато се умножи по отрицателно число неравенство признаци са разменени:
Препишете във възходящ ред
Добавяне на срока от мандат 4
Най-високата експресия стойност е равна на 7 (най - 1, диапазона на стойности - [1, 7]).
Най-високата експресия стойност е равна на 10 (най-малката - 8, обхвата на стойности - [8, 10]).
(Забележка: Ако на пред-конвертирате изразът .:
възможно е да се опрости оценката, тъй като не е необходимо да се умножи на неравенството с отрицателно число) в този случай.
Решение: Фракция има смисъл, ако знаменателят не е нула, така че DHS: sinα ≠ 0. Предпочитаният работа с DHS на единица кръг: точките α = 0 и α = P, в които sinα изчезва. пункции:
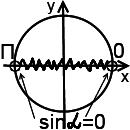
Остава да се прецени израз получава.
Въпреки това, предвид на ДХС, ние имаме:
(Cosα = 1 за α = 0, cosα = -1 когато α = P).
Изразът не поема максимална или малките стойности (площ на експресионни стойности - (8; 10)).
Следващият път, ще продължи да се помисли изразите с фракции, както и по-късно - изрази на формата на ∙ sinα + б ∙ cosα.