Пирамида в която ъглите между равнините наравно

А сега да разгледаме пирамидата, в която ъглите между равнините, в основата са равни на това, което техните свойства са представени.

Ако всички двустенни ъгли в краищата на основата са равни. на

1) на върха на пирамидата се очаква в центъра на кръга, вписан в основата;

2) основата на пирамидата е ортогонална проекция на неговата странична повърхност. обаче пирамида базова площ може да се намери с формула

- на двустенен ъгъл в основата на пирамидата. В повечето случаи тази формула се използва за намиране областта на страничната повърхност на пирамидата:

Следователно, общата площ на пирамидата е

3) странична повърхност в този случай може да се намери с формула

където р - semiperimeter база, л - височина на страничната ръб съставен от върха на пирамидата.

В правоъгълни триъгълници, образувани от височината на пирамидата, височината на страничните стени, съставени от върха на пирамидата и техните издатини (равни на радиуса на вписан кръг) са равни. Затова и

- височината на страничните повърхности, изготвени от върха на пирамидата, са равни;

- височината на страничните повърхности, които са пирамида с равни ъгли височина.

Решаването на проблемите в една пирамида, в която ъглите между равнините, в основата, равна на (или - пирамида, в която височината на страничните стени са формирани или с височина равни ъгли пирамида), започва с чертежа.

Ако основата на пирамидата - триъгълник

а центърът вписан в триъгълника лежи строго в рамките на триъгълника и пресечна точка на ъглополовящи него.

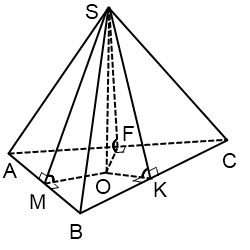
Радиусът на вписан кръг търси формула

където S - площта на триъгълника, стр - подът й периметър.

Ако основата на пирамидата е правоъгълен триъгълник. изготвяне малко по-различно.

Това се дължи на свойствата на едновременно проектиране: директен паралелизъм се поддържа. Радиусите перпендикулярна катет и сегменти, съседен на десния ъгъл на триъгълник, квадрат форма, която е показана на успоредник на чертеж.

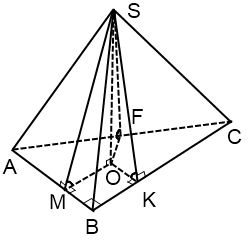
Радиусът на кръга вписан в правоъгълен триъгълник търси формула

където А и Б - на крака, век - хипотенузата.

Ако основата на пирамидата - успоредник

От всички Parallelograms впише окръжност е възможно само в диаманта (и квадрат като специален случай). Ето защо, ако един проблем е известно, че всички ъглите между равнините на равна основа (или височината на страничните части на пирамидите се формират и от двете височина на пирамидата равни ъгли), а основата е успоредник, а след това може да се говори само на диаманта (или квадратна).

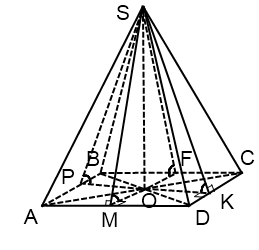
О - точката на пресичане на диагоналите на ромб (квадрат).

Радиусът на вписан кръг в диамант може да се намери по формулата

Освен това радиусът на вписан кръг в ромба е половината от височината.

Ако основата на пирамидата - произволен четириъгълник

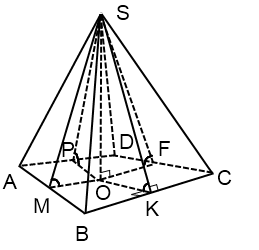
За - точката на пресичане на ъглополовящи на четириъгълник ABCD.

Радиусът на кръга вписан в четириъгълника търси същата формула

Както е вписан в четириъгълник кръг може да бъде единствено и само ако сумата от дължините на противоположните страни са равни,

Ако основата на пирамидата - Keystone

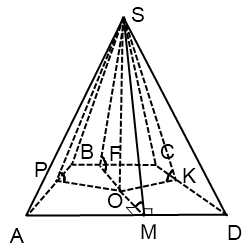
О - точката на пресичане на ъглополовящи на трапеца.

Радиусът на окръжността, вписан в трапец

и радиуса на вписан кръга е равен на половината от височината на трапеца.

Ако всички двустенни ъгли в основата на пирамидата са равни (или височината на страничните стени на пирамидата са равни, или височината на страничните стени на пирамидата направи равни ъгли), а в дъното на пирамидата - правилен многоъгълник, това е - редовен пирамида.